

分析 (1)图1,过P作PC∥直线a,根据平行线的性质得到∠1=∠APC,∠2=∠BPC,于是得到结论;
(2)如图2,由已知条件得到四边形MQNP是平行四边形,根据平行四边形的性质得到∠MQN=∠P=∠1+∠2,根据平角的定义即可得到结论;
(3)由垂直的定义得到∠QEP=90°,由平行线的性质得到∠QFE=∠P,根据平角的定义得到结论.
解答  解:(1)图1,过P作PC∥直线a,
解:(1)图1,过P作PC∥直线a,
∴PC∥b,
∴∠1=∠APC,∠2=∠BPC,
∴∠2=∠APB-∠1=41°;
故答案为:41;
(2)如图2,∵QM∥PB,QN∥PA,
∴四边形MQNP是平行四边形,
∴∠MQN=∠P=∠1+∠2,
∴∠EQN=180°-∠MQM=180°-∠1-∠2;
即∠Q=∠1+∠2或,∠Q=180°-∠1-∠2;
(3)∵QE⊥AP,
∴∠QEP=90°,
∵QF∥PB,
∴∠QFE=∠P,
∴∠EQF=90°-∠QFE=90°-∠1-∠2,
∴∠EQG=180°-∠EQF=90°+∠1+∠2.
点评 本题考查了平行线的性质,平行四边形的判定和性质,平角的定义,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
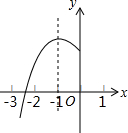 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com