
 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.分析 (1)利用等腰三角形的性质结合三角形内角和定理得出∠BAO+∠GAE=90°,进而得出答案;
(2)利用锐角三角函数关系得出BC=$\frac{8}{cos37°}$即可得出答案.
解答 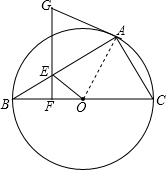 解:(1)AG与⊙O相切,
解:(1)AG与⊙O相切,
证明:如图 连接OA,
∵OA=OB,GA=GE,
∴∠ABO=∠BAO,∠GEA=∠GAE.
∵EF⊥BC,
∴∠BFE=90°.
∴∠ABO+∠BEF=90°.
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF.
∴∠BAO+∠GAE=90°.
∴OA⊥AG,即AG与⊙O相切.
(2)∵BC为直径,
∴∠BAC=90°,
在Rt△BAC中,∠BAC=90°.
∵BA=8,∠B=37°,
∴BC=$\frac{8}{cos37°}$≈10.02.
点评 此题主要考查了切线的性质以及锐角三角函数关系,正确应用切线的性质是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3,6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3,6或6.5或5.4时,△ACP是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线AB∥CD,AO,CO分别是∠BAC和∠ACD的角平分线,则∠OAC和∠OCA之间的大小关系一定为( )
如图,直线AB∥CD,AO,CO分别是∠BAC和∠ACD的角平分线,则∠OAC和∠OCA之间的大小关系一定为( )| A. | 互余 | B. | 互补 | C. | 相等 | D. | 不等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 共青团县委准备在艺术节期间举办学生绘画展览,为美化画面,在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图所示),若设彩纸的宽度为xcm,则列方程整理成一般形式为x2+25x-150=0.
共青团县委准备在艺术节期间举办学生绘画展览,为美化画面,在长30cm、宽20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图所示),若设彩纸的宽度为xcm,则列方程整理成一般形式为x2+25x-150=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题:画图并填空:
作图题:画图并填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2x+5=\frac{1}{x}$ | B. | 3x-2y=6 | C. | $\frac{x}{2}=5-x$ | D. | x2+2x=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com