
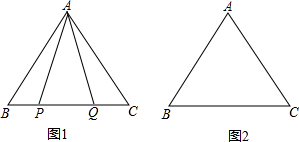
分析 (1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
(2)如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
解答 解:(1)∵AP=AQ,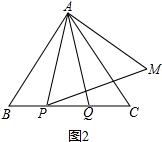
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=20°,
∴∠AQB=∠APQ=∠BAP+∠B=80°;
(2)如图2,∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ,(将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM)
∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°,
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
∴AP=PM.证明△ABP≌△ACM≌△BCK
点评 本题考查了等边三角形的性质和判定,等腰三角形的性质,三角形的外角的性质,轴对称的性质,熟练掌握等边三角形的判定和性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
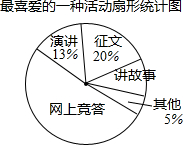 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:| 活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
| 人数 | 60 | 30 | 39 | a | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
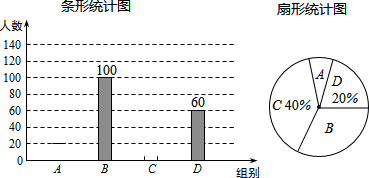
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
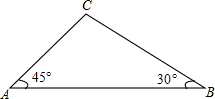 如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com