
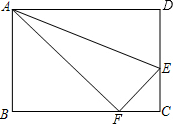
 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.
如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
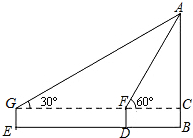 某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4,3) | B. | (-3,4) | C. | (3,-4) | D. | (4,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com