练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．命题“周长相等的两个三角形全等”是假命题．（填“真”或“假”）

    分析 根据全等三角形的判定方法可判定命题的真假．

    解答 解：命题“周长相等的两个三角形全等”是假命题．如边长分别为3、4、5的直角三角形与边长为4的等边三角形周长相等，但它们不全等．
    故答案为假．

    点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式． 有些命题的正确性是用推理证实的，这样的真命题叫做定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．下列图形不是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．若关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{5-2x＜1}\end{array}\right.$的整数解只有1个，则a的取值范围是（　　）
    A．2＜a＜3B．3≤a＜4C．2＜a≤3D．3＜a≤4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

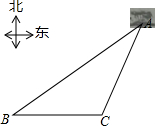    11．如图，在海中有一个小岛，在它周围6nmile有暗礁，渔船跟踪鱼群由西向东航行，在B处测得小岛A在北偏东55°方向，航行6n mile到达C点，这是测得小岛A在北偏东29°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？（参考数据：tan29°≈0.55，tan35°≈0.70，tan55°≈1.43，tan61°≈1.80）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

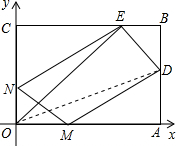    18．如图所示，已知OABC是一张放在平面直角坐标系中的矩形纸片，O为坐标原点，点A在x轴上，点C在y轴上，且OA=15，OC=9，在边AB上选取一点D，将△AOD沿OD翻折，使点A落在BC边上，记为点E．
    （Ⅰ）求点E和点D的坐标；
    （Ⅱ）在x轴、y轴上是否分别存在点M、N，使四边形MNED的周长最小？如果存在，求出点M、N的坐标及四边形MNED周长的最小值；如果不存在，请说明理由．
    （Ⅲ）设点P在x轴上，以点O、E、P为顶点的三角形是等腰三角形，请直接写出所有满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简，再求值：（2x-y）2+（6x3-8x2y+4xy2）÷（-2x），其中$x=\frac{2}{3}$，y=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．“十一”黄金周期间，某动物园在7天假期中每天旅游的人数变化如表：（正数表示比前一天多的人数，负数表示比前一天少的人数）．
    日期（10月）1日2日3日 4日5日6日7日
    人数变化
    单位：万人    		+1.6+0.8+0.4-0.4-0.8+0.2-1.2
    （1）若9月30日的游客人数记为a万人，则10月1日的游客人数为：（a+1.6）万人．（请用含a的代数式表示）
    （2）请问七天内游客人数最多的是哪天？最少的是哪天？（请说明理由）
    （3）若9月30日的游客人数为2万人，门票为每人10元，则黄金周期间该动物园门票收入是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算
    （1）$\sqrt{6}$×$\sqrt{\frac{2}{3}}$；
    （2）-$\sqrt{3}$•$\sqrt{（-16）（-36）}$；
    （3）$\sqrt{2}$×$\frac{1}{3}$$\sqrt{3}$•$\sqrt{6}$；
    （4）$\sqrt{\frac{a}{b}}$$÷\sqrt{ab}$•$\sqrt{\frac{1}{ab}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

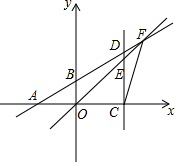    7．如图，点A、B坐标分别为A（-2，0），B（0，1），点E是坐标平面内的任意一点，过点E作x轴的垂线交x轴于点C，交直线AB于点D，直线OE交直线AB于点F，连接CF，若△CEF是一个有一内角为120°的等腰三角形，则符合条件的点E的有（　　）个．
    A．3个B．4个C．5个D．6个

    查看答案和解析>>

    同步练习册答案