如图.已知AB∥CD.BE平分∠ABC.DE平分∠ADC.∠BAD=80°.试求:(1)∠EDC的度数,(2)若∠BCD=n°.试求∠BED的度数. ∠BED=°. [解析][解析] ∵AB∥CD ∴∠ADC=∠BAD=80° ∵DE平分∠ABC ∴∠EDB=∠ADC=40° 过E作EF∥AB ∵AB∥CD ∴EF∥CD ∠DEF=∠EDC=40° ∵AB∥CD ∴∠ABC=∠BCD=n° ∵BE平分∠ABC � 题目和参考答案——青夏教育精英家教网—

如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，∠BAD=80°，试求：

（1）∠EDC的度数；

（2）若∠BCD=n°，试求∠BED的度数.(用含n的式子表示）

（1）∠EDC =40°；（2）∠BED=(40+n)°. 【解析】【解析】 ∵AB∥CD ∴∠ADC=∠BAD=80° ∵DE平分∠ABC ∴∠EDB=∠ADC=40° 过E作EF∥AB ∵AB∥CD ∴EF∥CD ∠DEF=∠EDC=40° ∵AB∥CD ∴∠ABC=∠BCD=n° ∵BE平分∠ABC ∴∠1=n° ∵AB∥EF ∴∠BEF=∠1=n...

练习册系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

赢在起跑线天天100分小学优化测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

△ABC是等腰三角形，腰上的高为8cm，面积为40cm2，则该三角形的周长是_______cm.

或. 【解析】（1）如图1，在△ABC中，AB=AC，∠A是锐角，BD是AC边上的高，由题意可知：BD=8cm，S△ABC=BD·AC=40cm2， ∴AC=10cm=BC， ∴在Rt△ABD中，由勾股定理可得：AD=（cm）， ∴DC=AC-AD=4cm， ∴在Rt△BDC中，由勾股定理可得：BC=（cm）， ∴此时△ABC的周长=AB+AC+BC=（...

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：解答题

某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A、B两组，采用不同工艺做降温对比实验，设降温开始后经过x min时，A、B两组材料的温度分别为yA℃、yB℃，yA、yB与x的函数关系式分别为yA=kx+b，yB=（x﹣60）2+m（部分图象如图所示），当x=40时，两组材料的温度相同．

（1）分别求yA、yB关于x的函数关系式；

（2）当A组材料的温度降至120℃时，B组材料的温度是多少？

（3）在0＜x＜40的什么时刻，两组材料温差最大？

【答案】（1）yA=﹣20x+1000；

（2）B组材料的温度是164℃；

（3）当x=20时，两组材料温差最大为100℃．

【解析】试题分析：（1）首先求出yB函数关系式，进而得出交点坐标，即可得出yA函数关系式；（2）首先将y=120代入求出x的值，进而代入yB求出答案；（3）得出yA-yB的函数关系式，进而求出最值即可．

试题解析：（1）由题意可得出：yB=（x﹣60）2+m经过（0，1000），

则1000=（0﹣60）2+m，

解得：m=100，

∴yB=（x﹣60）2+100，

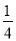当x=40时，yB=×（40﹣60）2+100，

解得：yB=200，

yA=kx+b，经过（0，1000），（40，200），

则，

解得：，

∴yA=﹣20x+1000；

（2）当A组材料的温度降至120℃时，

120=﹣20x+1000，

解得：x=44，

当x=44，yB=（44﹣60）2+100=164（℃），

∴B组材料的温度是164℃；

（3）当0＜x＜40时，yA﹣yB=﹣20x+1000﹣（x﹣60）2﹣100=﹣x2+10x=﹣（x﹣20）2+100，

∴当x=20时，两组材料温差最大为100℃．

【题型】解答题
【结束】
26

正方形ABCD的边长为6cm，点E，M分别是线段BD，AD上的动点，连接AE并延长，交边BC于F，过M作MN⊥AF，垂足为H，交边AB于点N.

(1)如图①，若点M与点D重合，求证：AF＝MN；

(2)如图②，若点M从点D出发，以1cm/s的速度沿DA向点A运动，同时点E从点B出发，以cm/s的速度沿BD向点D运动，运动时间为ts.

①设BF＝ycm，求y关于t的函数表达式；

②当BN＝2AN时，连接FN，求FN的长．

见解析【解析】试题分析：（1）根据四边形的性质得到AD=AB，∠BAD=90°，由垂直的定义得到∠AHM=90°，由余角的性质得到∠BAF=∠AMH，根据全等三角形的性质即可得到结论；（2）①根据勾股定理得到BD=6，由题意得，DM=t，BE=t，求得AM=6-t，DE=6-t，根据相似三角形的判定和性质即可得到结论； ②根据已知条件得到AN=2，BN=4，根据相似三角形的性...

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：单选题

如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若BO=6cm,OC=8cm 则BE+CG的长等于( )

A. 13 B. 12 C. 11 D. 10

D 【解析】根据切线长定理得：BE=BF，CF=CG，∠OBF=∠OBE，∠OCF=∠OCG； ∵AB∥CD， ∴∠ABC+∠BCD=180°， ∴∠OBF+∠OCF=90°， ∴∠BOC=90°， ∵OB=6cm，OC=8cm， ∴BC=10cm， ∴BE+CG=BC=10cm，故选D.

查看答案和解析>>

科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型：单选题

点A(-2,5)在反比例函数y= (k0)的图象上,则k的值是( )

A. B. C. -10 D. -5

C 【解析】把（-2，5）代入y=，得：，解得：k=-10，故选C.

查看答案和解析>>

科目：初中数学 来源：广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型：填空题

如图，函数与函数的图象交干点P关于x的方程的解是______；

x=1 【解析】试题解析：由图象可得：函数y=2x+b与函数y=kx?1的图象交于点P(1,?2)，关于x的方程解是：故答案为：

查看答案和解析>>

科目：初中数学 来源：广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型：单选题

深圳空气质量优良指数排名近年来一直排在全国城市前十.下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数（AQI）数据：

监测点	荔园	西乡	华侨城	南油	盐田	龙岗	洪湖	南澳	葵涌	梅沙	观澜
AQI	15	31	25	24	31	24	25	25	34	20	26
质量	优	优	优	优	优	优	优	优	优	优	优

上述（AQI）数据中，众数和中位数分别是（）

A. 25,25 B. 31,25 C. 25,24 D. 31,24

A 【解析】试题分析：一组数据中出现次数最多的数据叫做众数；把这组数据按照从小到大的顺序排列，第6个数是中位数．因此把这组数据按照从小到大的顺序排列15，20，24，24，25，25，25，26，31，31，34，第6个数是25，所以中位数是25；在这组数据中出现次数最多的是25，即众数是25．故选A．

查看答案和解析>>

科目：初中数学 来源：2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型：解答题

计算：

（1）；