
【题目】(探究与创新):已知A、B在数轴上分别表示a、b
①对照数轴填写下表:
a | 6 | ﹣6 | ﹣6 | 2 | ﹣1.5 |
b | 4 | 0 | ﹣4 | ﹣10 | ﹣1.5 |
A、B两点的距离 | 2 |
|
|
| 0 |
②若A、B两点间的距离记为d,则d和a、b之间有何数量关系?(直接写出结果)
③在数轴上标出所有符合条件的整数点P使它到5和﹣5的距离之和为10,并求出所有这些整数的和.
![]()
④若点Q表示的数为x,当点Q在什么位置时,|x+1|+|x﹣2|有最小值?最小值是多少?
【答案】①6,2,12;②d=|a﹣b|;③ 0;④当点Q在﹣1和2之间时,即﹣1≤x≤2时,|x+1|+|x﹣2|有最小值,最小值是3.
【解析】
① 用a,b对应的数相减,再取绝对值即可得出答案;
② 由①中的计算可以得出规律,从而得出答案;
③ 先根据5和-5之间的距离正好为10,可以确定5和-5之间的整数点都满足条件,然后在数轴上标出符合题意的点,再运用有理数的加法法则计算即可;
④ 根据绝对值的几何意义可得答案.
解:①当![]() 时,A,B两点间的距离为
时,A,B两点间的距离为![]() ,
,
当![]() 时,A,B两点间的距离为
时,A,B两点间的距离为![]() ,
,
当![]() 时,A,B两点间的距离为
时,A,B两点间的距离为![]() ;
;
②根据①中的结果可知,两点间的距离为这两点所表示的有理数之差的绝对值,即d=|a﹣b|.
③ ![]()
∴使5和﹣5的距离之和为10的整数点为-5,-4,-3,-2,-1,0,1,2,3,4,5,
数轴上表示如下:
![]()
﹣5﹣4﹣3﹣2﹣1+0+1+2+3+4+5=0
∴所有这些整数的和为0.
④ 根据题意可知,|x+1|+|x﹣2|可以看出x到-1和x到2的距离之和,当x在-1和2中间时,x到-1和x到2的距离之和最小,
∵﹣1到2的距离是:2﹣(﹣1)=3
∴当点Q在﹣1和2之间时,即﹣1≤x≤2时,|x+1|+|x﹣2|有最小值,最小值是3.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象顶点坐标为(1,4),且经过点C(3,0).
(1)求该二次函数的解析式;
(2)当x取何值时,y随x的增大而减小?
(3)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
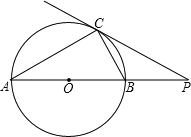
【题目】如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=![]() (90°﹣∠P)成立.请你写出推理过程.
(90°﹣∠P)成立.请你写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽泰州”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成该改造工作.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,若需改造的道路全长2400米,改造总费用不超过195万元,则至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
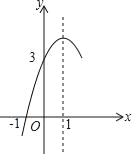
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
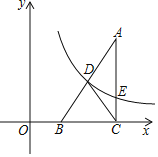
(1)求k的值;(2)若AE=BC,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
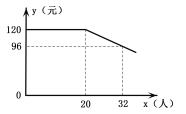
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:梯形ABCD中,∠ABC=90°,∠DAB=45°,AB∥DC,DC=3,AB=5,点P在AB边上,以点A为圆心AP为半径作弧交边DC于点E,射线EP于射线CB交于点F.

(1)若AP![]() ,求DE的长;
,求DE的长;
(2)联结CP,若CP=EP,求AP的长;
(3)线段CF上是否存在点G,使得△ADE与△FGE相似?若相似,求FG的值;若不相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com