
分析 (1)先移项,再把方程左边画出完全平方式的形式,利用直接开方法求出x的值即可;
(2)先移项,再把方程左边化为两个因式积的形式,求出x的值即可;
(3)先把方程化为一元二次方程的一般形式,求出x的值即可;
(4)直接利用平方差公式即可得出结论.
解答 解:(1)移项得,2x2-5x=-2
方程两边同时除以2得,x2-$\frac{5}{2}$x=-1,
配方得,x2-$\frac{5}{2}$x+(-$\frac{5}{4}$)2=-1+(-$\frac{5}{4}$)2,即(x-$\frac{5}{4}$)2=$\frac{9}{16}$
方程两边直接开方得,x-$\frac{5}{4}$=±$\frac{3}{4}$,
解得,x1=2,x2=$\frac{1}{2}$;
(2)移项,3x2-5x-2=0,
方程左边化为两个因式积的形式,( x-2 )( 3x+1 )=0,
故x-2=0 或 3x+1=0,
解得,x1=2,x2=-$\frac{1}{3}$;
(3)原方程可化为:2x2-4x=0,
提取公因式得,2x(x-2)=0,
故2x=0 或 x-2=0,
解得x1=0,x2=2;
(4)移项得,(x-2)2-(2x+3)2=0
因式分解得,(x-2+2x+3)(x-2-2x-3)=0,即(3x+1)(-x-5)=0,
故3x+1=0 或-x-5=0
解得,x1=-$\frac{1}{3}$,x2=-5.
点评 本题考查的是解一元二次方程,在解答此类问题时要注意根据方程的特点选取适当的解题方法.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
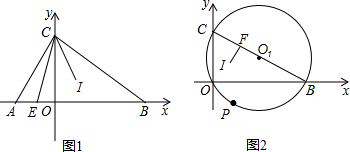
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2<a<-1 | B. | -2≤a<-1 | C. | -2<a≤-1 | D. | -2≤a≤-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com