

分析 (1)由AB=CD,BC=DA得到?ABCD,推出OA=OC,OB=OD,连接OM,∠AMC=∠BMD=90°,根据直角三角形斜边的中线等于斜边的一半,得到BD=AC,即可得出答案.
(2)由矩形的性质得出∠B=90°,由直角三角形的性质得出∠BGE=30°,由中点的定义和由折叠的性质得:EH=BE=AE,∠HEG=∠BEG=60°,∠BCE=∠HCE=30°,得出∠BCH=60°,∠AEH=60°,得出△AEH是等边三角形,得出∠AEH=∠EAH=∠AHE=60°,即可得出结论.
解答 (1)证明:连接OM,如图所示: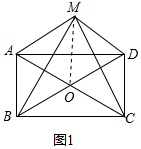
∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AM⊥MC,BM⊥MD,
∴∠AMC=∠BMD=90°,
∴OM=$\frac{1}{2}$BD,OM=$\frac{1}{2}$AC,
∴BD=AC,
∴四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,
∴∠B=90°,
∵∠BEG=60°,
∴∠BGE=30°,
∵点E是AB的中点,
∴AE=BE,
由折叠的性质得:EH=BE=AE,∠HEG=∠BEG=60°,∠BCE=∠HCE=30°,
∴∠BCH=60°,∠AEH=180°-60°-60°=60°,
∴△AEH是等边三角形,
∴∠AEH=∠EAH=∠AHE=60°,
∴图中与∠BEG相等的所有的角有∠AEH、∠EAH、∠AHE、∠GEH、∠BGH.
点评 本题考查了平行四边形的性质和判定,直角三角形斜边的中线,矩形的判定等知识点,解此题的关键是证出BD=AC,题目较好,综合性强.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
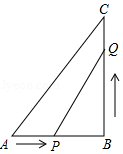 已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒,
已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.905×108 | B. | 2.905×109 | C. | 2.905×1010 | D. | 2.905×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
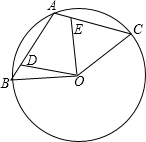 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com