
 已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,
已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,分析 (1)设AC=x,BC=4-x,根据等腰直角三角形性质,得出CD=$\frac{\sqrt{2}}{2}$x,CE=$\frac{\sqrt{2}}{2}$(4-x),根据勾股定理求出DE;
(2)把(1)中的DE与x的函数关系变形为顶点式,求出DE的最小值.
解答 解:(1)设AC=x,BC=4-x,
∵△ADC,△BCE均为等腰直角三角形,
∴CD=$\frac{\sqrt{2}}{2}$x,CE=$\frac{\sqrt{2}}{2}$(4-x),
∵∠ACD=45°,∠BCE=45°,
∴∠DCE=90°,
∴DE2=CD2+CE2=$\frac{1}{2}$x2+$\frac{1}{2}$(4-x)2=x2-4x+8,
∴DE=$\sqrt{{x}^{2}-4x+8}$;
(2)DE2=x2-4x+8=(x-2)2+4,
∴当x=2时,DE2取最小值4,
∴DE的最小值为2.
点评 本题考查了二次函数最值及等腰直角三角形,关键是根据勾股定理列出函数表达式并掌握用配方法求二次函数最值.


科目:初中数学 来源: 题型:选择题
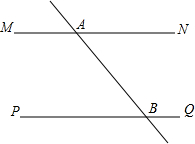 如图,公路MN∥PQ,公路AB交公路MN于A,交公路PQ于B,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )
如图,公路MN∥PQ,公路AB交公路MN于A,交公路PQ于B,若要建一汽车旅店到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
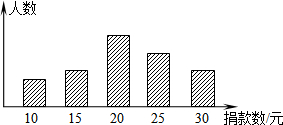 振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:8:6:4,又知此次调查中捐款20元和25元的学生共28人.
振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:8:6:4,又知此次调查中捐款20元和25元的学生共28人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com