有六张完全相同的卡片，分A、B两组，每组三张，在A组的卡片上分别画上√×√，B组的卡片上分别画上√××，如图1所示。
（1）若将卡片无标记的一面朝上摆在桌上，再发布从两组卡片中随机各抽取一张，求两张卡片上标记都是√的概率（请用树形图法或列表法求解）
（2）若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片，其正反面标记如图2所示，将卡片正面朝上摆放在桌上，并用瓶盖盖住标记。
①若随机揭开其中一个盖子
，看到的标记是√的概率是多少
②若揭开盖子，看到的卡片正面标记是√后，猜想它的反面也是√，求猜对的概率。
尖子生新课堂课时作业系列答案科目：初中数学 来源： 题型：
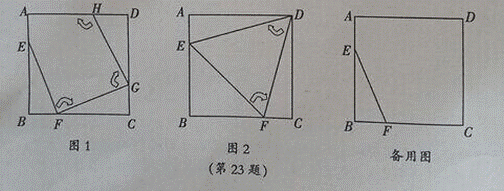
已知反比例函数y1=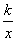
的图象与一次函数y2=ax+b的图象交于
点A（1，4）和点B（m，﹣2），
(1)求这两个函数的关系式；
(2)观察图象，写出使得y1＞y2成立的自变量x的取值范围；
(3)如果点C与点A关于x轴对称，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
下表是我市某一天在不同时段测得的气温情况
| 0：00 | 4：00 | 8：00 | 12：00 | 16：00 | 20：00 |
| 25℃ | 27℃ | 29℃ | 32℃ | 34℃ | 30℃ |
则这一天气温的极差是 ℃．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，边长为4的正方形ABCD中，点E在AB边上（不与点A、B重合），点F在BC边上（不与点B、C重合）
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；
第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；
依此操作下去
（1） 图2中的三角形EFD是经过两次操作后得到的，其形状为_______,求此时线段EF的长；
（2） 若经过三次操作可得到四边形EFGH的形状为_________,此时AE与BF的数量关系是_______;
① 请判断四边形EFGH的形状为______,此时AE与BF的数量关系是_______
② 以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图（2），AB是
⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=65°，则∠BOC=
|
查看答案和解析>>
科目：初中数学 来源： 题型：
|
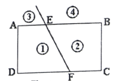
如图（13），E是直线AB、CD内部一点，AB∥CD，连接EA、ED （1）探究猜想： ①若∠A=30°，∠D=40°，则∠AED等于多少度？ ②若∠A=20°，∠D=60°，则∠AED等于多少度？ ③猜想图（13）中∠AED、∠EAB、∠EDC的关系并证明你的结论.
（2）拓展应用： 如图（14），射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③④位于直线AB上方），P是位于以上四个区域上点，猜想：∠PEB、∠PFC、∠EPF的关系（不要求证明）. | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图像如右图所示，则二次函数
的图像大致为（ ）
，AB=2，则图中阴影部分的面积为______
轴和
轴上，点B的坐标为
，双曲线
的图象经过BC的中点D，且于AB交于点E.