Question

已知2x+3=2a，y-2a=4，并且a-

3

4

＜x+y≤2a+

11

2

．
（1）求a的取值范围；
（2）化简：|2a-6|+2|a+2|的结果是

 

；
（3）比较a²+2a-5与a²+a-1的大小．

Answer 1

分析：（1）由已知的两等式分别解出x与y，代入已知的不等式中得到关于a的双向不等式，化为关于a的一元一次不等式组，分别求出两不等式的解集，利用不等式组取解集的方法即可求出不等式组的解集，进而得到a的范围；
（2）由（1）中求出的a的范围，判定得到2a-6与a+2的正负，根据绝对值的代数意义：正数的绝对值等于它本身；负数的绝对值等于它的相反数，0的绝对值还是0，即可把绝对值化简，合并后即可求出值；
（3）利用“作差法”，即第一个式子减去第二个式子，去括号合并后，由（1）得到的a的范围，判定其差小于0即可得到被减数小于减数，得到两式的大小关系．

解答：解：（1）由2x+3=2a，得到x=

2a-3

2

，由y-2a=4，得到y=2a+4，
代入a-

3

4

＜x+y≤2a+

11

2

得：a-

3

4

＜

2a-3

2

+2a+4≤2a+

11

2

，
可化为：

a- 3 4 ＜ 2a-3 2 +2a+4① 2a-3 2 +2a+4＜2a+ 11 2 ②

，
由①去分母得：4a-3＜4a-6+8a+16，即8a＞-13，解得a＞-

13

8

；
由②去分母得：2a-3+4a+8＜4a+11，即2a＜6，解得a＜3，
∴不等式组的解集为：-

13

8

＜a≤3；
（2）由（1）求出的a的范围得：2a-6≤0，a+2＞0，
则|2a-6|+2|a+2|=6-2a+2（a+2）=6-2a+2a+4=10；
（3）∵（a²+2a-5）-（a²+a-1）=a²+2a-5-a²-a+1=a-4＜0，
∴a²+2a-5＜a²+a-1．
故答案为：10．

点评：此题考查了整式的运算，以及一元一次不等式组的解法．不等式组的解法是以解一元一次不等式为基础，其步骤为：去分母，去括号，移项，合并同类项，系数化为“1”，本题的关键是把已知的不等式化为关于a的不等式组，求出不等式组的解集得到a的范围，第（2）、（3）都是借助a的范围，分别利用绝对值的代数意义及作差法来求解．
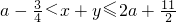