
 ;3;存在
;3;存在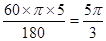 ;……4分
;……4分


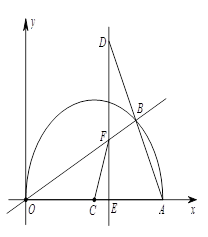
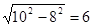 ,
,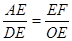 ,即
,即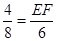 ,∴EF=3;……8分
,∴EF=3;……8分 ,
, ,0);
,0); ,
, ,即
,即 ,解得:
,解得: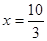 ,
, ,0);
,0);

 ,
, ,
, ,
, ,解得
,解得 ,
, <0(舍去),
<0(舍去), ,0);
,0);

 =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO ,
, ,
, ,
, ,解得
,解得 ,
, <0(舍去),
<0(舍去), ,0),
,0), (
( ,0)、
,0)、 (
( ,0)、
,0)、 (
( ,0)、
,0)、 (
( ,0).(12分)
,0).(12分)

 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源:不详 题型:解答题
 ,现将△DEF沿直线BC以每秒
,现将△DEF沿直线BC以每秒 个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒. ?若存在,试求出CH的值;若不存在,请说明理由.
?若存在,试求出CH的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
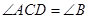 ;(2)
;(2)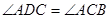 ;(3)
;(3)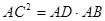 ;(4)
;(4)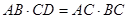 ,其中能判定△ACD∽△ABC的共有( )
,其中能判定△ACD∽△ABC的共有( )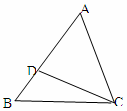
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.20 | B.7 | C.14 | D.12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.75cm2 | B.65cm2 | C.50cm2 | D.45cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com