
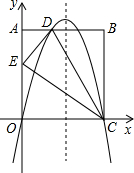
 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.分析 (1)由矩形的性质可求得C点坐标,再利用待定系数法可求得抛物线的解析式;
(2)用t可分别表示出CQ、PC的长,当∠PQC=∠DAE=90°,有△ADE∽△QPC;当∠QPC=∠DAE=90°,有△ADE∽△PQC,利用相似三角形的性质可分别得到关于t的方程,可求得t的值;
(3)由题意可知CE为平行四边形的对角线,根据抛物线的对称性可知当M为抛物线顶点时满足条件,再由平行四边形的性质可知线段MN被线段EC平分,可求得N点坐标.
解答 解:
(1)∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
∴C(8,0),
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0),
∴$\left\{\begin{array}{l}{9a+3b=10}\\{64a+8b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{16}{3}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{16}{3}$x;
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE,
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,
∴PC=10-2t.
当∠PQC=∠DAE=90°,△ADE∽△QPC,
∴$\frac{CQ}{AE}$=$\frac{CP}{DE}$,即$\frac{t}{4}$=$\frac{10-2t}{5}$,解得t=$\frac{40}{13}$.
当∠QPC=∠DAE=90°,△ADE∽△PQC,
∴$\frac{PC}{AE}$=$\frac{CQ}{DE}$,即$\frac{10-2t}{4}$=$\frac{t}{5}$,解得t=$\frac{25}{7}$.
∴当t的$\frac{40}{13}$或$\frac{25}{7}$时,以P、Q、C为顶点的三角形与△ADE相似;
(3)存在符合条件的M、N点,
EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,
若四边形MENC是平行四边形,那么M点必为抛物线顶点;
则M(4,$\frac{32}{3}$);
而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,
则N(4,-$\frac{14}{3}$);
∴存在符合条件的M、N点,且它们的坐标为M(4,$\frac{32}{3}$),N(4,-$\frac{14}{3}$).
点评 本题为二次函数的综合应用,涉及待定系数法、相似三角形的判定和性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中用t表示出CQ和CP的长,根据相似三角形的性质得到关于t的方程是解题的关键,在(3)中确定出M点的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲乙 | B. | 丙丁 | C. | 甲丁 | D. | 乙丙 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
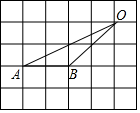 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
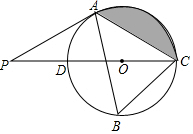 如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com