
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЮвУЧЖЈвхжБЯпy=ax-aЮЊХзЮяЯпy=ax2+bx+cЃЈaЁЂbЁЂcЮЊГЃЪ§ЃЌaЁй0ЃЉЕФЁАбмЩњжБЯпЁБЃЛгавЛИіЖЅЕудкХзЮяЯпЩЯЃЌСэгавЛИіЖЅЕудкyжсЩЯЕФШ§НЧаЮЮЊЦфЁАбмЩњШ§НЧаЮЁБЃЎвбжЊХзЮяЯп![]() гыЦфЁАбмЩњжБЯпЁБНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЎ
гыЦфЁАбмЩњжБЯпЁБНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЎ
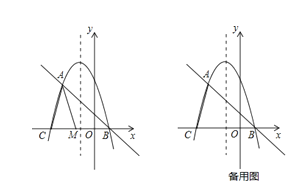
ЃЈ1ЃЉЬюПеЃКИУХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ ЃЌЕуAЕФзјБъЮЊ ЃЌЕуBЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉШчЭМЃЌЕуMЮЊЯпЖЮCBЩЯвЛЖЏЕуЃЌНЋЁїACMвдAMЫљдкжБЯпЮЊЖдГЦжсЗелЃЌЕуCЕФЖдГЦЕуЮЊNЃЌШєЁїAMNЮЊИУХзЮяЯпЕФЁАбмЩњШ§НЧаЮЁБЃЌЧѓЕуNЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуEдкХзЮяЯпЕФЖдГЦжсЩЯдЫЖЏЪБЃЌдкИУХзЮяЯпЕФЁАбмЩњжБЯпЁБЩЯЃЌЪЧЗёДцдкЕуFЃЌЪЙЕУвдЕуAЁЂCЁЂEЁЂFЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуEЁЂFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ-2ЃЌ
ЃЛЃЈ-2ЃЌ![]() ЃЉЃЛЃЈ1,0ЃЉЃЛ
ЃЉЃЛЃЈ1,0ЃЉЃЛ
ЃЈ2ЃЉNЕуЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉEЃЈ-1ЃЌ-![]() ЃЉЁЂFЃЈ0ЃЌ
ЃЉЁЂFЃЈ0ЃЌ![]() ЃЉЛђEЃЈ-1ЃЌ
ЃЉЛђEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХзЮяЯпЕФЁАбмЩњжБЯпЁБжЊЕРЖўДЮКЏЪ§НтЮіЪНЕФaМДПЩЃЛЃЈ2ЃЉЙ§AзїADЁЭyжсгкЕуDЃЌдђПЩжЊAN=ACЃЌНсКЯAЕузјБъЃЌдђПЩЧѓГіONЕФГЄЃЌПЩЧѓГіNЕуЕФзјБъЃЛЃЈ3ЃЉЗжБ№ЬжТлЕБACЮЊЦНааЫФБпаЮЕФБпЪБЃЌЕБACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌЧѓГіТњзуЬѕМўЕФEЁЂFзјБъМДПЩ
ЃЈ1ЃЉЁп![]() ЃЌa=
ЃЌa=![]() ЃЌдђХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ
ЃЌдђХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
СЊСЂСННтЮіЪНЧѓНЛЕу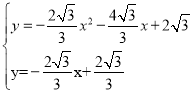 ЃЌНтЕУ
ЃЌНтЕУ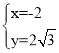 Лђ
Лђ![]() ЃЌ
ЃЌ
ЁрAЃЈ-2ЃЌ![]() ЃЉЃЌBЃЈ1,0ЃЉЃЛ
ЃЉЃЌBЃЈ1,0ЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§AзїADЁЭyжсгкЕуDЃЌ
дк![]() жаЃЌСюy=0ПЩЧѓЕУx= -3Лђx=1ЃЌ
жаЃЌСюy=0ПЩЧѓЕУx= -3Лђx=1ЃЌ
ЁрCЃЈ-3,0ЃЉЃЌЧвAЃЈ-2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAC=![]()
гЩЗелЕФаджЪПЩжЊAN=AC=![]() ЃЌ
ЃЌ
ЁпЁїAMNЮЊИУХзЮяЯпЕФЁАбмЩњШ§НЧаЮЁБЃЌ
ЁрNдкyжсЩЯЃЌЧвAD=2ЃЌ
дкRtЁїANDжаЃЌгЩЙДЙЩЖЈРэПЩЕУ
DN=![]() ЃЌ
ЃЌ
ЁпOD=![]() ЃЌ
ЃЌ
ЁрON=![]() ЛђON=
ЛђON=![]() ЃЌ
ЃЌ
ЁрNЕуЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
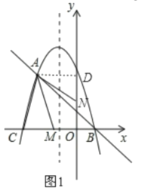
ЃЈ3ЃЉЂйЕБACЮЊЦНааЫФБпаЮЕФБпЪБЃЌШчЭМ2 ЃЌЙ§FзїЖдГЦжсЕФДЙЯпFHЃЌЙ§AзїAKЁЭxжсгкЕуKЃЌдђгаACЁЮEFЧвAC=EFЃЌ
ЁрЁЯ ACK=ЁЯ EFHЃЌ
дкЁї ACKКЭЁї EFHжа
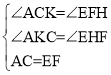
ЁрЁї ACKЁеЁї EFHЃЌ
ЁрFH=CK=1ЃЌHE=AK=![]() ЃЌ
ЃЌ
ЁпХзЮяЯпЕФЖдГЦжсЮЊx=-1ЃЌ
Ёр FЕуЕФКсзјБъЮЊ0Лђ-2ЃЌ
ЁпЕуFдкжБЯпABЩЯЃЌ
ЁрЕБFЕуЕФКсзјБъЮЊ0ЪБЃЌдђFЃЈ0ЃЌ![]() ЃЉЃЌДЫЪБЕуEдкжБЯпABЯТЗНЃЌ
ЃЉЃЌДЫЪБЕуEдкжБЯпABЯТЗНЃЌ
ЁрEЕНyжсЕФОрРыЮЊEH-OF=![]() -
-![]() =
=![]() ЃЌМДEЕФзнзјБъЮЊ-
ЃЌМДEЕФзнзјБъЮЊ-![]() ЃЌ
ЃЌ
Ёр EЃЈ-1ЃЌ-![]() ЃЉЃЛ
ЃЉЃЛ
ЕБFЕуЕФКсзјБъЮЊ-2ЪБЃЌдђFгыAжиКЯЃЌВЛКЯЬтвтЃЌЩсШЅЃЛ
ЂкЕБACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌ
Ёп CЃЈ-3,0ЃЉЃЌЧвAЃЈ-2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрЯпЖЮACЕФжаЕузјБъЮЊЃЈ-2.5ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшEЃЈ-1ЃЌtЃЉЃЌFЃЈxЃЌyЃЉЃЌ
дђx-1=2ЁСЃЈ-2.5ЃЉЃЌy+t=![]() ЃЌ
ЃЌ
Ёрx= -4ЃЌy=![]() -tЃЌ
-tЃЌ
![]() -t=-
-t=-![]() ЁСЃЈ-4ЃЉ+
ЁСЃЈ-4ЃЉ+![]() ЃЌНтЕУt=
ЃЌНтЕУt=![]() ЃЌ
ЃЌ
ЁрEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯПЩжЊДцдкТњзуЬѕМўЕФЕуFЃЌДЫЪБEЃЈ-1ЃЌ-![]() ЃЉЁЂЃЈ0ЃЌ
ЃЉЁЂЃЈ0ЃЌ![]() ЃЉЛђEЃЈ-1ЃЌ
ЃЉЛђEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉ
ЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂй
ЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЕФНтЮЊ
ЕФНтЮЊ![]() ЃЌЦфжае§ШЗЕФгаЃЈ ЃЉ
ЃЌЦфжае§ШЗЕФгаЃЈ ЃЉ
A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
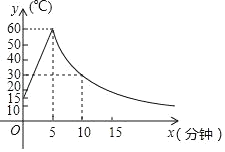
ЁОЬтФПЁПЙЄГЇЖдФГжжаТаЭВФСЯНјааМгЙЄЃЌЪзЯШвЊНЋЦфМгЮТЃЌЪЙетжжВФСЯБЃГждквЛЖЈЮТЖШЗЖЮЇФкЗНПЩМгЙЄЃЌШчЭМЪЧдкетжжВФСЯЕФМгЙЄЙ§ГЬжаЃЌИУВФСЯЕФЮТЖШyЃЈЁцЃЉЪБМфxЃЈminЃЉБфЛЏЕФЪ§ЭМЯѓЃЌвбжЊИУВФСЯЃЌГѕЪМЮТЖШЮЊ15ЁцЃЌдкЮТЖШЩЯЩ§НзЖЮЃЌyгыxГЩвЛДЮКЏЪ§ЙиЯЕЃЌдкЕк5ЗжжгЮТЖШДяЕН60ЁцКѓЭЃжЙМгЮТЃЌдкЮТЖШЯТНЕНзЖЮЃЌyгыxГЩЗДБШР§ЙиЯЕЃЎ
ЃЈ1ЃЉаДГіИУВФСЯЮТЖШЩЯЩ§КЭЯТНЕНзЖЮЃЌyгыxЕФКЏЪ§ЙиЯЕЪНЃК
ЂйЩЯЩ§НзЖЮЃКЕБ0ЁмxЁм5ЪБЃЌyЃНЁЁ ЁЁЃЛ
ЂкЯТНЕНзЖЮЃКЕБxЃО5ЪБЃЌyЁЁ ЁЁЃЎ
ЃЈ2ЃЉИљОнЙЄвевЊЧѓЃЌЕБВФСЯЕФЮТЖШВЛЕЭгк30ЁцЃЌПЩвдНјааВњЦЗМгЙЄЃЌЧыЮЪдкЭМжаЫљЪОЕФЮТЖШБфЛЏЙ§ГЬжаЃЌПЩвдНјааМгЙЄЖрГЄЪБМфЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжжЩЬЦЗЕФБъМлЮЊ500дЊ/МўЃЌОЙ§СНДЮНЕМлКѓЕФМлИёЮЊ405дЊ/МўЃЌВЂЧвСНДЮНЕМлЕФАйЗжТЪЯрЭЌЃЎ
ЃЈ1ЃЉЧѓИУжжЩЬЦЗУПДЮНЕМлЕФАйЗжТЪЃЛ
ЃЈ2ЃЉШєИУжжЩЬЦЗНјМлЮЊ400дЊ/МўЃЌСНДЮНЕМлЙВЪлГіДЫжжЩЬЦЗ100МўЃЌЮЊЪЙСНДЮНЕМлЯњЪлЕФзмРћШѓВЛЩйгк3200дЊЃЎЮЪЕквЛДЮНЕМлКѓжСЩйвЊЪлГіИУжжЩЬЦЗЖрЩйМўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЃ3ЃЌ2ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ

ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁї![]() CЃЛЦНвЦЁїABCЃЌШєAЕФЖдгІЕу
CЃЛЦНвЦЁїABCЃЌШєAЕФЖдгІЕу![]() ЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁї
ЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁї![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєНЋЁї![]() CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁї
CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁї![]() ЃЌЧыжБНгаДГіа§зЊжааФЕФзјБъЃЛ
ЃЌЧыжБНгаДГіа§зЊжааФЕФзјБъЃЛ
ЃЈ3ЃЉдк![]() жсЩЯгавЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
жсЩЯгавЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧBCЕФжаЕуЃЌСЌНгDEЃЌЙ§ЕуAзїAGЁЭEDНЛDEгкЕуFЃЌНЛCDгкЕуGЃЎ
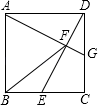
ЃЈ1ЃЉжЄУїЃКЁїADGЁеЁїDCEЃЛЃЈ2ЃЉСЌНгBFЃЌжЄУїЃКABЃНFBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2+bx+cгыyжсНЛгкЕуAЃЈ0ЃЌ2ЃЉЃЌЖдГЦжсЮЊжБЯпx=Љ2ЃЌЦНаагкxжсЕФжБЯпгыХзЮяЯпНЛгкBЁЂCСНЕуЃЌЕуBдкЖдГЦжсзѓВрЃЌBC=6ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЕуPдкxжсЩЯЃЌжБЯпCPНЋЁїABCУцЛ§ЗжГЩ2ЃК3СНВПЗжЃЌЧыжБНгаДГіPЕузјБъЃЎ
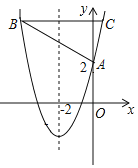
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНЉx2+x+6МАвЛДЮКЏЪ§yЃНx+mЃЌНЋИУЖўДЮКЏЪ§дкxжсЩЯЗНЕФЭМЯѓбиxжсЗелЕНxжсЯТЗНЃЌЭМЯѓЕФЦфгрВПЗжВЛБфЃЌЕУЕНвЛИіаТЭМЯѓЃЈШчЭМЫљЪОЃЉЃЌЕБжБЯпyЃНx+mгыетИіаТЭМЯѓгаЫФИіНЛЕуЪБЃЌmЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
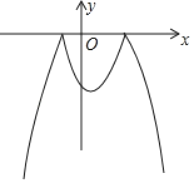
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cЃЌЕБxЃН3ЪБЃЌyгазюаЁжЕЉ4ЃЌЧвЭМЯѓОЙ§Еу(Љ1ЃЌ12)ЃЎ
(1)ЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)ИУХзЮяЯпНЛxжсгкЕуAЃЌB(ЕуAдкЕуBЕФзѓВр)ЃЌНЛyжсгкЕуCЃЌдкХзЮяЯпЖдГЦжсЩЯгавЛЖЏЕуPЃЌЧѓPA+PCЕФзюаЁжЕЃЌВЂЧѓЕБPA+PCШЁзюаЁжЕЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com