[题目]在平面直角坐标系中.把一条抛物线先向上平移3个单位长度.然后绕原点旋转180°得到抛物线y=x2+5x+6.则原抛物线的解析式是( )A. y=﹣(x﹣)2﹣ B. y=﹣(x+)2﹣C. y=﹣(x﹣)2﹣ D. y=﹣(x+)2+ 题目和参考答案——青夏教育精英家教网—

【题目】在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y=x2+5x+6，则原抛物线的解析式是（）

A. y=﹣（x﹣）2﹣ B. y=﹣（x+）2﹣

C. y=﹣（x﹣）2﹣ D. y=﹣（x+）2+

【答案】A

【解析】试题分析：已知抛物线的解析式为y=x2+5x+6，设原抛物线上有点（x，y），绕原点旋转180°后，变为（﹣x，﹣y），点（﹣x，﹣y）在抛物线y=x2+5x+6上，将（﹣x，﹣y）代入y=x2+5x+6得﹣y=x2﹣5x+6，所以原抛物线的方程为y=﹣x2+5x﹣6=﹣（x﹣）2+，所以向下平移3个单位长度的解析式为y=﹣（x﹣）2+﹣3=﹣（x﹣）2﹣．故选A．

练习册系列答案

考必胜小学毕业升学考试试卷精选系列答案

精华版中考备战策略系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，点O为坐标原点，直线y=﹣x+3与x轴、y轴相交于B、C两点，抛物线y=ax2+bx+3经过点B，对称轴为直线x=1．

（1）求a和b的值；

（2）点P是直线BC上方抛物线上任意一点，设点P的横坐标为t，△PBC的面积为S，求S与t之间的函数关系式，并写出t的取值范围；

（3）P为抛物线上的一点，连接AC，当∠BCP=∠ACO时，求点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件．市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．

（1）求w与x之间的函数关系式，并写出自变量x的取值范围；

（2）该产品销售价定为每件多少元时，每星期的销售利润最大？最大利润是多少元？

（3）该产品销售价在什么范围时，每星期的销售利润不低于6000元，请直接写出结果．

查看答案和解析>>

科目：初中数学 来源： 题型：

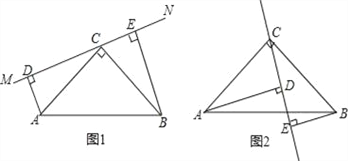
【题目】如图（1）在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．求证：

（1）△ADC≌△CEB；

（2）DE=AD+BE．

（3）当直线MN绕点C旋转到图（2）的位置时，DE、AD、BE又怎样的关系？并加以证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】附加题：已知数轴上两点A，B对应的数分别为﹣1、3，点P为数轴上一动点，其对应的数为x．

（1）若点P到点A，点B的距离相等，求点P对应的数；
（2）数轴上是否存在点P，使点P到点A，点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由；
（3）点A，点B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？