
【题目】已知函数f(x)=ln2(x﹣1)﹣ ![]() ﹣x+3. (Ⅰ)求函数f(x)的单调区间;
﹣x+3. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若当x≥1时,不等式(x+1)x+m≤exx+m恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)由f(x)=ln2(x﹣1)﹣ ![]() ﹣x+3, 得f′(x)=
﹣x+3, 得f′(x)= ![]() ln(x﹣1)+
ln(x﹣1)+ ![]() ﹣1=
﹣1= ![]()
= ![]() (x﹣1>0),
(x﹣1>0),
令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,
g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,
再令t(x)=2ln(x﹣1)﹣2x+4,
t′(x)= ![]() ,当x∈(1,2)时,t′(x)>0,t(x)为增函数,
,当x∈(1,2)时,t′(x)>0,t(x)为增函数,
当x∈(2,+∞)时,t′(x)<0,t(x)为减函数,
∴t(x)max=t(2)=0,
∴g′(x)≤0,则g(x)在(1,+∞)上为减函数,
又当x→1+时,g(x)→﹣∞,
∴f′(x)<0,
则f(x)在(1,+∞)上为单调减函数;
(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,
∴(x+m)ln ![]() ≤1,也即x+m
≤1,也即x+m ![]() ,
,
∴m ![]() 对x≥1恒成立.
对x≥1恒成立.
令h(x)= ![]() ,
,
则h′(x)= 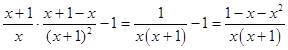 <0(x≥1),
<0(x≥1),
∴h(x)在[1,+∞)上为减函数,则h(x)≤h(1)=﹣ln2﹣1,
又当x→+∞时,h(x)→﹣∞,
∴h(x)在[1,+∞)上无最小值,
则满足m ![]() 对x≥1恒成立的m不存在.
对x≥1恒成立的m不存在.
【解析】(Ⅰ)求出原函数的导函数,可得f′(x)= ![]() (x﹣1>0),令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,求导可得g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,再令t(x)=2ln(x﹣1)﹣2x+4,利用导数求得t(x)max=t(2)=0,得g′(x)≤0,则g(x)在(1,+∞)上为减函数,进一步说明f′(x)<0,得到f(x)在(1,+∞)上为单调减函数;(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,分离参数m,可得m
(x﹣1>0),令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,求导可得g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,再令t(x)=2ln(x﹣1)﹣2x+4,利用导数求得t(x)max=t(2)=0,得g′(x)≤0,则g(x)在(1,+∞)上为减函数,进一步说明f′(x)<0,得到f(x)在(1,+∞)上为单调减函数;(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,分离参数m,可得m ![]() 对x≥1恒成立.令h(x)=
对x≥1恒成立.令h(x)= ![]() ,由导数求其值域,可知h(x)在[1,+∞)上无最小值,则满足m
,由导数求其值域,可知h(x)在[1,+∞)上无最小值,则满足m ![]() 对x≥1恒成立的m不存在.
对x≥1恒成立的m不存在.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]()
![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: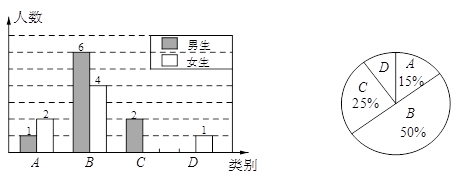
(1)李老师一共调查了多少名同学?
(2)C类女生有名,D类男生有名,将下面条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行
“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣1|,(m>0),且f(x+1)≥0的解集为[﹣3,3]. (Ⅰ)求m的值;
(Ⅱ)若正实数a,b,c满足 ![]() ,求证:a+2b+3c≥3.
,求证:a+2b+3c≥3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点, ![]()

(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ![]() ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
(1)若点A1的坐标为(2,1),则点A4的坐标为_____;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足 ![]() =
= ![]() ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com