
【题目】如图,若每个小正方形的边长均为1,试解决以下问题:

(1)图中阴影部分的面积是多少?
(2)阴影部分正方形的边长是多少?
(3)估计边长的值在哪两个整数之间?
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
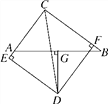
【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣6×(﹣3)+2×(﹣4) ; (2)﹣16﹣(﹣5)+23﹣|﹣![]() |
|
(3)﹣(1﹣0.5)÷![]() ×[2+(﹣4)2].
×[2+(﹣4)2].
(4)(4)﹣22﹣(﹣![]() )2×
)2×![]() +6÷|
+6÷|![]() ﹣2|+(﹣1)5×(﹣
﹣2|+(﹣1)5×(﹣![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
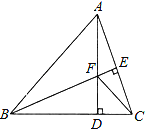
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com