
 如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
 数形结合”的基础.
数形结合”的基础.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
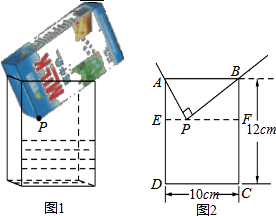 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com