
 2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:分析 (1)由于线段AB与x轴平行,故自3时到4.9时这段时间内甲组停留在途中,所以停留的时间为1.9时;
(2)观察图象可知点B的纵坐标就是甲组的汽车在排除故障时距出发点的路程的千米数,所以求得点B的坐标是解答(2)题的关键,这就需要求得直线EF和直线BD的解析式,而EF过点(1.25,0),(7.25,480),利用这两点的坐标即可求出该直线的解析式,然后令x=6,即可求出点C的纵坐标,又因点D(7,480),这样就可求出CD即BD的解析式,从而求出B点的坐标;
(3)由图象可知:甲、乙两组第一次相遇后在B和D相距最远,在点B处时,x=4.9,求出此时的y乙-y甲,在点D有x=7,也求出此时的y甲-y乙,分别同25比较即可.
解答 解:(1)观察图象可知:甲组在途中停留了4.9-3=1.9小时;
故答案为1.9.
(2)设直线EF的解析式为y乙=kx+b,
∵点E(1.25,0)、点F(7.25,480)均在直线EF上,
∴$\left\{\begin{array}{l}{1.25k+b=0}\\{7.25k+b=480}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=80}\\{b=-100}\end{array}\right.$,
∴直线EF的解析式是y乙=80x-100;
∵点C在直线EF上,且点C的横坐标为6,
∴点C的纵坐标为80×6-100=380;
∴点C的坐标是(6,380);
设直线BD的解析式为y甲=mx+n;
∵点C(6,380)、点D(7,480)在直线BD上,
∴$\left\{\begin{array}{l}{6m+n=380}\\{7m+n=480}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=100}\\{n=-220}\end{array}\right.$;
∴BD的解析式是y甲=100x-220;
∵B点在直线BD上且点B的横坐标为4.9,代入y甲得B(4.9,270),
∴甲组在排除故障时,距出发点的路程是270千米.
(3)符合约定;
由图象可知:甲、乙两组第一次相遇后在B和D相距最远.
在点B处有y乙-y甲=80×4.9-100-(100×4.9-220)=22千米<25千米,
在点D有y甲-y乙=100×7-220-(80×7-100)=20千米<25千米,
∴按图象所表示的走法符合约定.
点评 本题是依据函数图象提供的信息,解答相关的问题,充分体现了“数形结合”的数学思想,是中考的常见题型,其关键是认真观察函数图象、结合已知条件,正确地提炼出图象信息.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
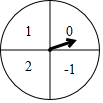 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 73 | B. | 74 | C. | 75 | D. | 76 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
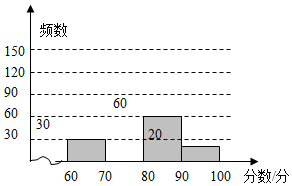 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x≤100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
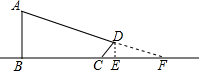 小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2-2x-a.
已知抛物线y=x2-2x-a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:
如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com