
����Ŀ����֪,����ABCD��,AB=4cm,BC=8cm,AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E. F,����ΪO.

(1)��ͼ1������AF��CE.��֤���ı���AFCEΪ����.
(2)��ͼ1����AF�ij�.
(3)��ͼ2������P��Q�ֱ��A. C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܡ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���P���ٶ�Ϊÿ��1cm�����˶�ʱ��Ϊt��.
�������˶��Ĺ����У���A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ�����?���п��ܣ�������˶�ʱ��t�͵�Q���ٶȣ��������ܣ���˵������.
������Q���ٶ�Ϊÿ��0.8cm����A. P��C. Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ.
���𰸡���1������������2��AF=5cm����3����P���˶���ʱ���� 8��Q���ٶ���0.5cm/s����t=![]() .
.
��������
��1��֤��AEO�ա�CFO���Ƴ�OE=OF������ƽ���ı��κ����ε��ж��Ƴ����ɣ�
��2����AF=CF=a�����ݹ��ɶ����ó�����a�ķ��̣�������ɣ�
��3����ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��Σ����ʱ��t����������𰸣��ڷ�Ϊ���������P��AF�ϣ�P��BF�ϣ�P��AB�ϣ�����ƽ���ı��ε�����������ɣ�
(1)֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���AEO=��CFO��
��AC�Ĵ�ֱƽ����EF��
��AO=OC��AC��EF��
����AEO����CFO��
�� ��
��
���AEO�ա�CFO(AAS)��
��OE=OF��
��OA=OC��
���ı���AECF��ƽ���ı��Σ�
��AC��EF��
��ƽ���ı���AECF�����Σ�
(2)��AF=acm��
���ı���AECF�����Σ�
��AF=CF=acm��
��BC=8cm��
��BF=(8a)cm��
��Rt��ABF��,�ɹ��ɶ����ã�4![]() +(8a)
+(8a) ![]() =a
=a![]() ��
��
a=5��
��AF=5cm��
(3)�����˶������У���A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
P���˶���ʱ���ǣ�(5+3)��1=8��
Q���ٶ��ǣ�4��8=0.5��
��Q���ٶ���0.5cm/s��
�ڷ�Ϊ���������
��һ��P��AF�ϣ�
��P���ٶ���1cm/s����Q���ٶ���0.8cm/s��
��Qֻ����CD�ϣ���ʱ��A. P��C. Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
�ڶ�����P��BF��ʱ,Q��CD��DE��,ֻ�е�Q��DE��ʱ,��A. P��C. Q�ĵ�Ϊ������ı��β��п�����ƽ���ı���,��ͼ,

��AQ=8(0.8t4),CP=5+(t5)��
��8(0.8t4)=5+(t5)��
t=![]() ��
��
�����������P��AB��ʱ��Q��DE��CE�ϣ���ʱ��A. P��C. Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
��t=![]() .
.
������������A. P��C. Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ,t=![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90����AB=4��AC=6����D��E�ֱ���BC��AD���е㣬AF��BC��CE���ӳ�����F�����ı���AFBD�����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��B��C���������������ֱ���a��b��1����|a��1|��|1��b|��|a��b|�������ĸ�ѡ���У��У����������ܱ�ʾA��B��C�����������ϵ�λ�ù�ϵ��
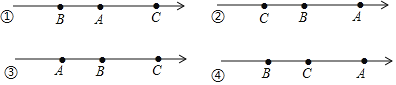
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
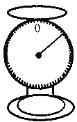
����Ŀ��ij�г��Ĺ�ƽ����ͼ,��10ǧ�˵IJ˷ŵ�����,ָʾ���ϵ�ָ��ת��180��.
(1)�����2.75ǧ�˵IJ˷��ڳ���,ָ��ת�����ٶ�?
(2)����ƺ�0.5ǧ�˵IJ�û������,�ٰ�һ���˷��ڳ���,ָ�빲ת��![]() ��ô,����ϵ��������ж���ǧ��?
��ô,����ϵ��������ж���ǧ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
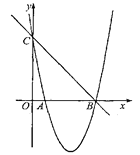
����Ŀ����ͼ����֪������y��x2��bx��c��ͼ����x���һ������ΪA(1��0)����һ������ΪB������y�ύ�ڵ�C(0��5)��
(1)��ֱ��BC�������ߵĽ���ʽ��
(2)����M����������x���·�ͼ���ϵ�һ���㣬����M��MN��y�ύֱ��BC�ڵ�N����MN�����ֵ��
(3)��(2)�������£�MNȡ�����ֵʱ������P����������x���·�ͼ��������һ�㣬��BCΪ������CBPQ������CBPQ�����ΪS1����ABN�����ΪS2����S1��6S2�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��y=2x+3��ֱ��y=��2x��1.

��1������ֱ����y�ύ��A��B�����ꣻ
��2������ֱ�߽���C�����ꣻ
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
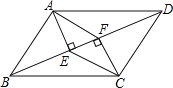
����Ŀ����ͼ�����ı���ABCD�У�AB��CD��BF=DE,AE��BD��CF��BD������ֱ�ΪE��F��
(1)��֤����ABE�ա�CDF��
(2)��AC��BD���ڵ�O����֤��AC��BD����ƽ�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��˫����![]() �ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ
�ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ
�����ȱ�������ABC����C�ڵ������ޣ���֪��C��λ��ʼ����һ����ͼ�����˶��������������
��ʽΪ�� ��
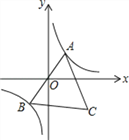
A. y=��![]() B. y=��
B. y=��![]() ��x��0�� C. y=��6x��x��0�� D. y= 6x��x��0��
��x��0�� C. y=��6x��x��0�� D. y= 6x��x��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
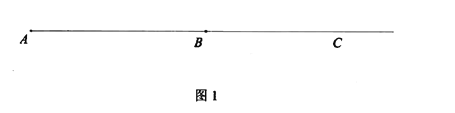
����Ŀ����ͼ1����![]() Ϊ�߶�
Ϊ�߶�![]() �ӳ����ϵ�һ�㣬��
�ӳ����ϵ�һ�㣬��![]() ��
��![]() ���е㣬�ҵ�
���е㣬�ҵ�![]() �����
�����![]() �غϣ�
�غϣ�![]() ����
����![]() ��
��
![]() ����
����![]() ����ͼ2����
����ͼ2����![]() ��
��
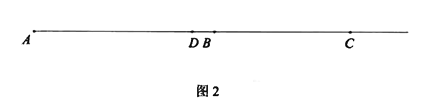
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���ֱ��д���𰸣�
�ij���ֱ��д���𰸣� ![]() ��
��![]() ��
��
![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() ������˵����
������˵����![]() ���߶�
���߶�![]() ���е���
�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com