
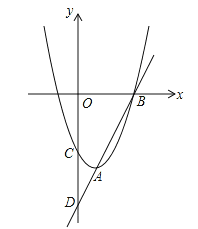
【题目】如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点
A(1,-4)为抛物线的顶点,点B在x轴上.直线AB交y轴于点D,抛物线交y轴于点C.
(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)在y轴上是否存在点Q,使△ABQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
【答案】(1)y=2x-6,(2)y=x2-2x-3;(3)(0,-![]() )或(0,
)或(0,![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).
【解析】
试题分析:(1)把点A坐标代入y=kx-6,根据待定系数法即可求得直线AB的解析式;
(2)根据直线AB的解析式求出点B的坐标,点A是抛物线的顶点,那么可以将抛物线的解析式设为顶点式,再代入点B的坐标,依据待定系数法即可求解;
(3)分别以A、B、Q为直角顶点,分类进行讨论.找出相关的相似三角形,依据对应线段成比例进行求解即可.
试题解析:(1)把A(1,-4)代入y=kx-6,得k=2,
∴直线AB的解析式为y=2x-6,
(2)∵抛物线的顶点为A(1,-4),
∴设此抛物线的解析式为y=a(x-1)2-4,
∵点B在直线y=2x-6上,且横坐标为0,
∴点B的坐标为(3,0),
又∵点B在抛物线y=a(x-1)2-4上,
∴a(3-1)2-4=0,解之得a=1,
∴此抛物线的解析式为y=(x-1)2-4,即y=x2-2x-3;
(3)在y轴上存在点Q,使△ABQ为直角三角形.理由如下:
作AE⊥y轴,垂足为点E.
又∵点D是直线y=2x-6与y轴的交点,点C是抛物线y=x2-2x-3与y轴的交点
∴E(0,-4),D(0,-6),C(0,-3)
∴OD=6,OE=4,AE=1,ED=2,OC=3,OB=3,BD=![]() ,AD=
,AD=![]()
①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,
∴![]() ,即
,即![]() ,
,
∴DQ1=![]() ,
,
∴OQ1=6-![]() =
=![]() ,即Q1(0,-
,即Q1(0,-![]() );
);
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴![]() ,即
,即![]() ,
,
∴OQ2=![]() ,即Q2(0,
,即Q2(0,![]() );
);
③如图,当∠AQ3B=90°时,则△BOQ3∽△Q3EA,
∴![]() ,即
,即![]() ,
,
∴OQ32-4OQ3+3=0,
∴OQ3=1或3,
即Q3(0,-1),Q4(0,-3).
综上,Q点坐标为(0,-![]() )或(0,
)或(0,![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
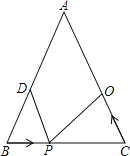
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
(3)若∠C=70°,当∠CPQ的度数为多少时,△CPQ为等腰三角形?(请直接写出答案,不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点门票价格规定如下:

某校七年级组织甲、乙两个班共92人去该景点游玩,其中甲班人数多余乙班人数且甲班人数不够90人,如果两个班单独购买门票,一共应付7760元.
(1)如果甲、乙两个班联合起来购买门票,那么比各自购买门票可以节省多少钱?
(2)甲、乙两个班各有多少学生?
(3)如果甲班有10名学生因学校有任务不能参加这次旅游,请你作为两个班设计出购买门票的方案,并指出最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.
(1)求中巴车和大客车各有多少个座位?
(2)客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1是二次函数y=x2﹣10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;交x轴于点A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…
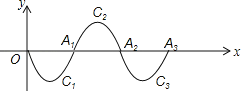
(1)抛物线C3与x轴的交点A3的坐标是多少?抛物线Cn与x轴的交点An的坐标是多少?
(2)若某段抛物线上有一点P(2016,a),试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com