
ЁОЬтФПЁПГЄЩГЪаНЬг§ОжзщжЏВПЗжНЬЪІЗжБ№ЕНAЁЂBЁЂCЁЂDЫФИіЕиЗННјааПЮГЬХрбЕЃЌНЬг§ОжАДЖЈЖюЙКТђСЫЧАЭљЫФЕиЕФГЕЦБЃЌШчЭМ1ЪЧЮДжЦзїЭъГЩЕФГЕЦБжжРрКЭЪ§СПЕФЬѕаЮЭГМЦЭМЃЌЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬтЃК
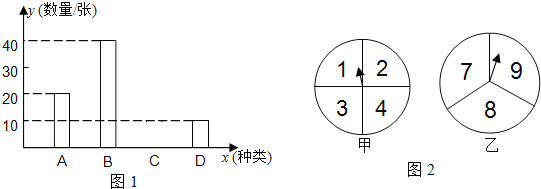
ЃЈ1ЃЉШєШЅAЕиЕФГЕЦБеМШЋВПГЕЦБЕФ20%ЃЌЧѓШЅCЕиЕФГЕЦБЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЈЭМ1ЃЉЃЛ
ЃЈ2ЃЉЧыДгаЁЕНДѓаДГіетЫФРрГЕЦБЪ§ЕФЪ§зжЃЌВЂжБНгаДГіетЫФИіЪ§ОнЕФЦНОљЪ§КЭжаЮЛЪ§ЃЛ
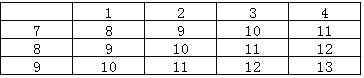
ЃЈ3ЃЉШчЭМ2ЃЌМззЊХЬБЛЗжГЩЫФЕШЗнЧвБъгаЪ§зж1ЁЂ2ЁЂ3ЁЂ4ЃЌввзЊХЬЗжГЩШ§ЕШЗнЧвБъгаЪ§зж7ЁЂ8ЁЂ9ЃЌОпЬхЙцЖЈЪЧЃКЭЌЪБзЊЖЏСНИізЊХЬЃЌЕБжИеыжИЯђЕФСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЃЌРюРЯЪІГіШЅХрбЕЃЌЗёдђеХРЯЪІГіШЅХрбЕЃЈжИеыжИдкЯпЩЯжизЊЃЉЃЌЪдгУЁАСаБэЗЈЁБЛђЁАЪїзДЭМЁБЕФЗНЗЈЗжЮіетИіЙцЖЈЖдЫЋЗНЪЧЗёЙЋЦНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ30еХЃЌМћНтЮіЃЛЃЈ2ЃЉ10ЁЂ20ЁЂ30ЁЂ40ЃЌЦНОљЪ§ЮЊ25ЃЌжаЮЛЪ§ЮЊ25ЃЛЃЈ3ЃЉЙЋЦНЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШгЩШЅAЕиЕФГЕЦБеМШЋВПГЕЦБЕФ20%ЧѓГіГЕЦБзмЪ§ЃЌзмЪ§СПМѕШЅAЁЂBЁЂDЕФЪ§СПМДПЩЧѓЕУCЕФЪ§СПЃЌДгЖјВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉНЋЫФИіЪ§зжДгаЁЕНДѓХХСаЃЌИљОнЦНОљЪ§КЭжаЮЛЪ§ЕФИХФюЧѓНтПЩЕУЃЛ
ЃЈ3ЃЉИљОнЬтвтгУСаБэЗЈЗжБ№ЧѓГіЕБжИеыжИЯђЕФСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЕФИХТЪЃЌМДПЩЧѓГіетИіЙцЖЈЖдЫЋЗНЪЧЗёЙЋЦНЃЎ
НтЃКЃЈ1ЃЉЁпШЋВПГЕЦБЪ§ЮЊ20ЁТ20%ЃН100ЃЈеХЃЉЃЌ
ЁрШЅCЕиГЕЦБЪ§ЮЊ100ЉЃЈ20+40+10ЃЉЃН30ЃЈеХЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
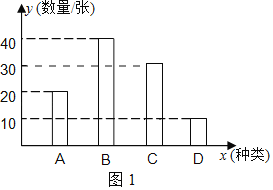
ЃЈ2ЃЉДгаЁЕНДѓаДГіетЫФРрГЕЦБЪ§ЕФЪ§зжЮЊЃК10ЁЂ20ЁЂ30ЁЂ40ЃЌ
дђетЫФИіЪ§ОнЕФЦНОљЪ§ЮЊ![]() ЃН25ЃЌжаЮЛЪ§ЮЊ
ЃН25ЃЌжаЮЛЪ§ЮЊ![]() ЃН25ЃЛ
ЃН25ЃЛ
ЃЈ3ЃЉИљОнЬтвтСаБэШчЯТЃК
вђЮЊСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЕФИХТЪЪЧ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрРюРЯЪІГіШЅХрбЕЕФИХТЪКЭеХРЯЪІГіШЅХрбЕЕФИХТЪЯрЕШЃЌОљЮЊ![]() ЃЌ
ЃЌ
ЙЪетИіЙцЖЈЖдЫЋЗНЪЧЙЋЦНЕФЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
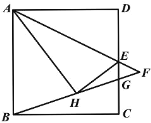
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌABЃН2ЃЌЕуEЪЧCDЕФжаЕуЃЌСЌНгAEЃЌНЋЁїADEбиAEелЕўжСЁїAHEЃЌСЌНгBHЃЌбгГЄAEЃЌBHНЛгкЕуFЃЛBFЃЌCDНЛгкЕуGЃЌдђFG=_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЮЊжЇГжДѓбЇЩњДДвЕЃЌЬсЙЉаЁЖюЮоЯЂДћПюЃЌбЇЩњЭѕЗМЯэЪмеўВпЮоЯЂДћПю![]() дЊгУРДДњРэЦЗХЦЗўзАЕФЯњЪлЃЎвбжЊИУЦЗХЦЗўзАНјМлУПМў
дЊгУРДДњРэЦЗХЦЗўзАЕФЯњЪлЃЎвбжЊИУЦЗХЦЗўзАНјМлУПМў![]() дЊЃЌШеЯњЪл
дЊЃЌШеЯњЪл![]() ЃЈМўЃЉгыЯњЪлМл
ЃЈМўЃЉгыЯњЪлМл![]() ЃЈдЊ/МўЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЈЪЕЯпЃЉЃЌУПЬьИЖдБЙЄЕФЙЄзЪУПШЫУПЬь
ЃЈдЊ/МўЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЈЪЕЯпЃЉЃЌУПЬьИЖдБЙЄЕФЙЄзЪУПШЫУПЬь![]() дЊЃЌУПЬьгІжЇИЖЦфЫќЗбгУ
дЊЃЌУПЬьгІжЇИЖЦфЫќЗбгУ![]() дЊЃЎ
дЊЃЎ

![]() ЧѓШеЯњЪл
ЧѓШеЯњЪл![]() ЃЈМўЃЉгыЯњЪлМл
ЃЈМўЃЉгыЯњЪлМл![]() ЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ШєднВЛПМТЧЛЙДћЃЌЕБФГЬьЕФЯњЪлМлЮЊ
ШєднВЛПМТЧЛЙДћЃЌЕБФГЬьЕФЯњЪлМлЮЊ![]() дЊ/МўЪБЃЌЪежЇЧЁКУЦНКтЃЈЪеШы
дЊ/МўЪБЃЌЪежЇЧЁКУЦНКтЃЈЪеШы![]() жЇГіЃЉЃЌЧѓИУЕъдБЙЄШЫЪ§ЃЛ
жЇГіЃЉЃЌЧѓИУЕъдБЙЄШЫЪ§ЃЛ
![]() ШєИУЕъжЛга
ШєИУЕъжЛга![]() УћдБЙЄЃЌдђИУЕъжСЩйашвЊЖрЩйЬьВХФмЛЙЧхДћПюЃЌДЫЪБЃЌУПМўЗўзАЕФМлИёгІЖЈЮЊЖрЩйдЊЃП
УћдБЙЄЃЌдђИУЕъжСЩйашвЊЖрЩйЬьВХФмЛЙЧхДћПюЃЌДЫЪБЃЌУПМўЗўзАЕФМлИёгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЛЊЮФУїЃЌдДдЖСїГЄЃЌжаЛЊККзжЃЌдЂвтЩюЙу.ЮЊДЋГажаЛЊгХауДЋЭГЮФЛЏЃЌФГжабЇЕТг§ДІзщжЏСЫвЛДЮШЋаЃ2000УћбЇЩњВЮМгЕФЁАККзжЬ§аДЁБДѓШќ.ЮЊСЫНтБОДЮДѓШќЕФГЩМЈЃЌбЇаЃЕТг§ДІЫцЛњГщШЁСЫЦфжа200УћбЇЩњЕФГЩМЈзїЮЊбљБОНјааЭГМЦЃЌжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэЃК
ГЩМЈxЃЈЗжЃЉЗжЪ§ЖЮ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
50Ёмx<60 | 10 | 0.05 |
60Ёмx<70 | 30 | 0.15 |
70Ёмx<80 | 40 | 0.2 |
80Ёмx<90 | m | 0.35 |
90Ёмx<100 | 50 | n |
ЦЕЪ§ЗжВМжБЗНЭМ

ИљОнЫљИјЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉm=________ЃЛn=________ЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉет200УћбЇЩњГЩМЈЕФжаЮЛЪ§ЛсТфдк________ЗжЪ§ЖЮЃЛ
ЃЈ4ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈАќРЈ90ЗжЃЉЮЊЁАгХЁБЕШЃЌЧыФуЙРМЦИУаЃВЮМгБОДЮБШШќЕФ2000УћбЇЩњжаГЩМЈЪЧЁАгХЁБЕШЕФдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
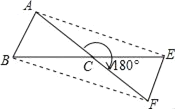
ЁОЬтФПЁПНЋЁїABCШЦЕуCа§зЊ180ЁуЕУЕНЁїFECЃЎ
ЃЈ1ЃЉЪдВТЯыAEгыBFгаКЮЙиЯЕЃПЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЁїABCЕФУцЛ§ЮЊ3cm2ЃЌЧѓЫФБпаЮABFEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдкЯпЖЮMNЩЯДцдкЕуPЁЂQНЋЯпЖЮMNЗжЮЊЯрЕШЕФШ§ВПЗжЃЌдђГЦPЁЂQЮЊЯпЖЮMNЕФШ§ЕШЗжЕуЃЎ
вбжЊвЛДЮКЏЪ§yЃНЉx+3ЕФЭМЯѓгыxЁЂyжсЗжБ№НЛгкЕуMЁЂNЃЌЧвAЁЂCЮЊЯпЖЮMNЕФШ§ЕШЗжЕуЃЈЕуAдкЕуCЕФзѓБпЃЉЃЎ
ЃЈ1ЃЉжБНгаДГіЕуAЁЂCЕФзјБъЃЛ
ЃЈ2ЃЉЂйЖўДЮКЏЪ§ЕФЭМЯѓЧЁКУОЙ§ЕуOЁЂAЁЂCЃЌЪдЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЂкЙ§ЕуAЁЂCЗжБ№зїABЁЂCDДЙжБxжсгкBЁЂDСНЕуЃЌдкДЫХзЮяЯпOЁЂCжЎМфШЁвЛЕуPЃЈЕуPВЛгыOЁЂCжиКЯЃЉзїPFЁЭxжсгкЕуFЃЌPFНЛOCгкЕуEЃЌЪЧЗёДцдкЕуPЪЙЕУAPЃНBEЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃПШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЁїOABбиACЗНЯђвЦЖЏЕНЁїO'A'B'ЃЈЕуA'дкЯпЖЮACЩЯЃЌЧвВЛгыCжиКЯЃЉЃЌЁїO'A'B'гыЁїOCDжиЕўВПЗжЕФУцЛ§ЮЊSЃЌЪдЧѓЕБSЃН![]() ЪБЕуA'ЕФзјБъЃЎ
ЪБЕуA'ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌ BCНЛЁбOгкЕуDЃЌEЪЧ![]() ЕФжаЕуЃЌСЌНгAEНЛBCгкЕуFЃЌЁЯACB =2ЁЯEABЃЎ
ЕФжаЕуЃЌСЌНгAEНЛBCгкЕуFЃЌЁЯACB =2ЁЯEABЃЎ
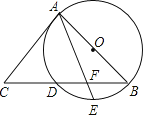
ЃЈ1ЃЉЧѓжЄЃКACЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓBFЕФГЄЃЎ
ЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉжЄУїЭЦЖЯЃКШчЭМЃЈ1ЃЉЃЌдке§ЗНаЮABCDжаЃЌЕуEЃЌQЗжБ№дкБпBCЃЌABЩЯЃЌDQЁЭAEгкЕуOЃЌЕуGЃЌFЗжБ№дкБпCDЃЌABЩЯЃЌGFЁЭAEЃЎ
ЂйЧѓжЄЃКDQЃНAEЃЛ
ЂкЭЦЖЯЃК![]() ЕФжЕЮЊЁЁ ЁЁЃЛ
ЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉРрБШЬНОПЃКШчЭМЃЈ2ЃЉЃЌдкОиаЮABCDжаЃЌ![]() ЃНkЃЈkЮЊГЃЪ§ЃЉЃЎНЋОиаЮABCDбиGFелЕўЃЌЪЙЕуAТфдкBCБпЩЯЕФЕуEДІЃЌЕУЕНЫФБпаЮFEPGЃЌEPНЛCDгкЕуHЃЌСЌНгAEНЛGFгкЕуOЃЎЪдЬНОПGFгыAEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃНkЃЈkЮЊГЃЪ§ЃЉЃЎНЋОиаЮABCDбиGFелЕўЃЌЪЙЕуAТфдкBCБпЩЯЕФЕуEДІЃЌЕУЕНЫФБпаЮFEPGЃЌEPНЛCDгкЕуHЃЌСЌНгAEНЛGFгкЕуOЃЎЪдЬНОПGFгыAEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙгІгУЃКдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгCPЃЌЕБkЃН![]() ЪБЃЌШєtanЁЯCGPЃН
ЪБЃЌШєtanЁЯCGPЃН![]() ЃЌGFЃН2
ЃЌGFЃН2![]() ЃЌЧѓCPЕФГЄЃЎ
ЃЌЧѓCPЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
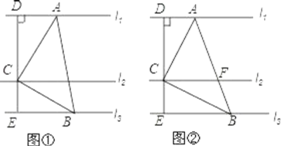
ЁОЬтФПЁПЬНОПЃКШчЭМЂйЃЌжБЯпl1ЁЮl2ЁЮl3ЃЌЕуCдкl2ЩЯЃЌвдЕуCЮЊжБНЧЖЅЕузїЁЯACBЃН90ЁуЃЌНЧЕФСНБпЗжБ№НЛl1гыl3гкЕуAЁЂBЃЌСЌНсABЃЌЙ§ЕуCзїCDЁЭl1гкЕуDЃЌбгГЄDCНЛl3гкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁзЁїCBEЃЎ
ЃЈ2ЃЉгІгУЃКШчЭМЂкЃЌдкЭМЂйЕФЛљДЁЩЯЃЌЩшABгыl2ЕФНЛЕуЮЊFЃЌШєACЃНBCЃЌl1гыl2жЎМфЕФОрРыЮЊ2ЃЌl2гыl3жЎМфЕФОрРыЮЊ1ЃЌдђAFЕФГЄЖШЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com