
 如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为$\frac{15}{4}$或$\frac{195}{4}$.
如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为$\frac{15}{4}$或$\frac{195}{4}$. 分析 连接BD交AC于O,由四边形ABCD是菱形,得到AC⊥BD,推出△AMP∽△AOB,①当CE=CB时,如图1,则CE=10,AE=6,AM=3,根据相似三角形的性质得到AP=$\frac{15}{4}$;②当BE=EC时,如图2,点E是BC的垂直平分线与AC的交点,则CF=5根据相似三角形的性质得到AP=$\frac{39×5}{8×4}$=$\frac{195}{32}$;③当BC=BE时,E与A重合;于是得到结论.
解答  解:连接BD交AC于O,
解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵PQ⊥AC,AO=$\frac{1}{2}$AC=8,
∴PQ∥BD,
∴△AMP∽△AOB,
①当CE=CB时,如图1,则CE=10,AE=6,AM=3,
∵△AMP∽△AOB,
∴$\frac{AP}{AB}$=$\frac{AM}{AO}$,
∴AP=$\frac{15}{4}$;
②当BE=EC时,如图2,点E是BC的垂直平分线与AC的交点,则CF=5,∵△CEF∽△CBO,
∴CE=$\frac{5×5}{4}$=$\frac{25}{4}$,∴AE=16-$\frac{25}{4}$=$\frac{39}{4}$,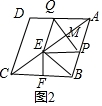
∴AM=$\frac{39}{8}$,
∴AP=$\frac{39×5}{8×4}$=$\frac{195}{32}$;
③当BC=BE时,E与A重合;
综上所述:当△BCE是等腰三角形时,AP的长为$\frac{15}{4}$或$\frac{195}{4}$.
故答案为:$\frac{15}{4}$或$\frac{195}{4}$.
点评 本题考查菱形的性质、翻折变换、等腰三角形的判定和性质、相似三角形的判定与性质、勾股定理等知识,解题的关键是学会分类讨论,不能漏解,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.
如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种 项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/每棚) |
| 香瓜 | 2000 | 12 | 8000 |
| 甜瓜 | 4500 | 3 | 5000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com