
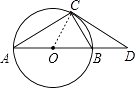
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB= ![]() CD,求⊙O半径.
CD,求⊙O半径.
【答案】
(1)证明:如图,连接CO,
 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,
x,
∵∠OCD=90°,
∴OD= ![]() =
= ![]() =
= ![]() x,
x,
∴BD=OD﹣OB= ![]() x﹣
x﹣ ![]() x=
x= ![]() x,
x,
由(1)知,△ADC∽△CDB,
∴ ![]() =
= ![]() ,
,
即 ![]() ,
,
解得CB=1,
∴AB= ![]() =
= ![]() ,
,
∴⊙O半径是 ![]()
【解析】(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.(2)首先设CD为x,则AB= ![]() x,OC=OB=
x,OC=OB= ![]() x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:
x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得: ![]() =
= ![]() ,据此求出CB的值是多少,即可求出⊙O半径是多少.
,据此求出CB的值是多少,即可求出⊙O半径是多少.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( ) 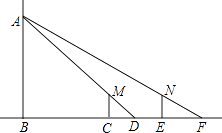
A.4.5米
B.6米
C.7.2米
D.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们的生活,如图所示的是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,有下列说法:其中正确说法的个数有( ) ①“快车”行驶里程不超过5公里计费8元;
②“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
③A点的坐标为(6.5,10.4);
④从合肥西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 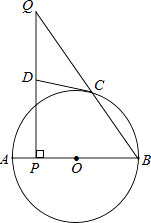
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ![]() ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 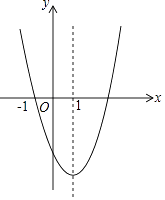
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( ) ①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PAPB=PCPD.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=﹣ ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 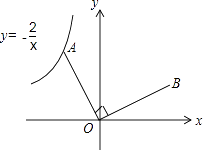
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com