
【题目】将正方形ABCD与等腰直角三角形EFG如图摆放,若点M、N刚好是AD的三等分点,下列结论正确的是( )
①△AMH≌△NME;②![]() ;③GH⊥EF;④S△EMN:S△EFG=1:16
;③GH⊥EF;④S△EMN:S△EFG=1:16
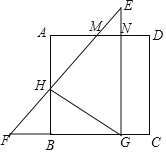
A.①②③④B.①②③C.①③④D.①②④
【答案】A
【解析】
利用三角形全等和根据题目设未知数,列等式解答即可.
解:设AM=x,
∵点M、N刚好是AD的三等分点,
∴AM=MN=ND=x,
则AD=AB=BC=3x,
∵△EFG是等腰直角三角形,
∴∠E=∠F=45°,∠EGF=90°,
∵四边形ABCD是正方形,
∴∠A=∠ABC=∠BGN=∠ABF=90°,
∴四边形ABGN是矩形,
∴∠AHM=∠BHF=∠AMH=∠NME=45°,
∴△AMH≌△NMH(ASA),故①正确;
∵∠AHM=∠AMH=45°,
∴AH=AM=x,
则BH=AB﹣AH=2x,
又Rt△BHF中∠F=45°,
∴BF=BH=2x,![]() =
=![]() ,故②正确;
,故②正确;
∵四边形ABGN是矩形,
∴BG=AN=AM+MN=2x,
∴BF=BG=2x,
∵AB⊥FG,
∴△HFG是等腰三角形,
∴∠FHB=∠GHB=45°,
∴∠FHG=90°,即GH⊥EF,故③正确;
∵∠EGF=90°、∠F=45°,
∴EG=FG=BF+BG=4x,
则S△EFG=![]() EGFG=
EGFG=![]() 4x4x=8x2,
4x4x=8x2,
又S△EMN=![]() ENMN=
ENMN=![]() xx=
xx=![]() x2,
x2,
∴S△EMN:S△EFG=1:16,故④正确;
故选A.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解某型导弹杀伤力的情况应使用全面调查
B.可能性是1%的事件在一次试验中一定不会发生
C.一组数据3、6、6、7、9的众数是6
D.甲,乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是![]() =0.3,
=0.3,![]() =0.4,则乙的成绩更稳定
=0.4,则乙的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是( )
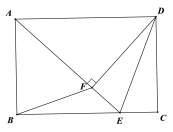
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
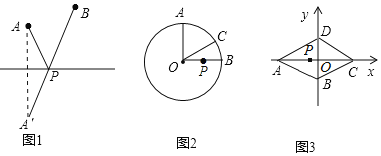
【题目】阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题﹣﹣如图1,从A点出发,到笔直的河岸l去饮马,然后再去B地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B 的值最小.
解答问题:
(1)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(2)如图3,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.
①为使点P能在最短的时间内到达点B处,则点M的位置应如何确定?
②在①的条件下,设点P的运动时间为t(s),△PAB的面积为S,在整个运动过程中,试求S与t之间的函数关系式,并指出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
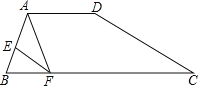
(1)求CF的长;
(2)若∠BFE=∠FAB,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
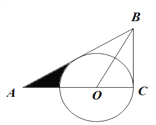
【题目】如图,△ABC中,∠C=90,∠ABC=2∠A,点O在AC上,OA=OB,以O为圆心,OC为半径作圆.
(1)求证:AB是⊙O的切线;
(2)若BC=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE连接BE

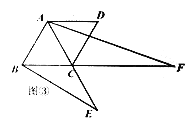
(1)发现问题:如图①,若E是线段AC的中点,连接EF,其他条件不变,猜想线段BE与EF的数量关系
(2)探究问题:如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想
(3)解决问题:如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=3请直接写出AF的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com