
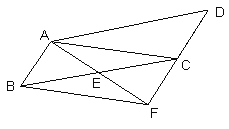
【题目】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
【答案】(1)见解析;(2)当BC=AF时,四边形ABFC是矩形,理由见解析
【解析】
(1)根据平行四边形的性质得到两角一边对应相等,利用AAS判定△ABE≌△FCE,从而得到AB=CF;
(2)由已知可得四边形ABFC是平行四边形,BC=AF,根据对角线相等的平行四边形是矩形,可得到四边形ABFC是矩形.
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴![]() ,
, ![]()
∵E为BC的中点
∴BE=EC
∴ △ABE≌△FCE
∴ AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.理由如下:
∵AB∥CF,AB=CF
∴四边形ABFC是平行四边形
∵BC=AF
∴四边形ABFC是矩形.


科目:初中数学 来源: 题型:
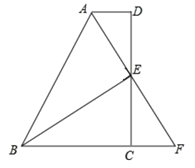
【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为平面直角坐标系的原点,在矩形
为平面直角坐标系的原点,在矩形![]() 中,两边
中,两边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,且点
轴上,且点![]() 满足:
满足:![]() .
.


(1)求点![]() 的坐标(___,_____);
的坐标(___,_____);
(2)若过点![]() 的直线
的直线![]() 与矩形
与矩形![]() 的
的![]() 边交于点
边交于点![]() ,且将矩形
,且将矩形![]() 的面积分为
的面积分为![]() 两部分,
两部分,
①求直线![]() 的解析式;
的解析式;
②在直线![]() 确定一点
确定一点![]() ,使得
,使得![]() 的面积等于矩形
的面积等于矩形![]() 的面积,求点
的面积,求点![]() 的坐标;
的坐标;
(3)![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 在坐标轴上,
在坐标轴上,![]() 为(2)中直线
为(2)中直线![]() 上一动点,若四点
上一动点,若四点![]() 、
、![]() 、
、![]() 、
、![]() 构成平行四边形,直接写出
构成平行四边形,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如12=![]() ,20=
,20=![]() ,28=
,28=![]() ,……,因此12,20,28这三个数都是奇巧数。
,……,因此12,20,28这三个数都是奇巧数。
(1)52,72都是奇巧数吗?为什么?
(2)设两个连续偶数为2n,2n+2(其中n为正整数),由这两个连续偶数构造的奇巧数是8的倍数吗?为什么?
(3)研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连结
,连结![]() 、
、![]() .
.
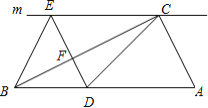
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若点![]() 是
是![]() 中点,当四边形
中点,当四边形![]() 是正方形时,则
是正方形时,则![]() 大小满足什么条件?
大小满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山是某市民周末休闲爬山的好去处,但总有些市民随手丢垃圾的情况出现.为了美化环境,提高市民的环保意识,某外国语学校某附属学校青年志愿者协会组织50人的青年志愿者团队,在周末前往临某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡130件垃圾.请问该团队的男生和女生各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com