
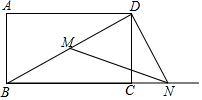
 已知,矩形ABCD中,AB=15,AD=20,点M在对角线BD上,点N为射线BC上一动点,连接MN、DN,且∠DNM=∠DBC,当DMN是等腰三角形,线段BN的长是25,40,$\frac{125}{8}$.
已知,矩形ABCD中,AB=15,AD=20,点M在对角线BD上,点N为射线BC上一动点,连接MN、DN,且∠DNM=∠DBC,当DMN是等腰三角形,线段BN的长是25,40,$\frac{125}{8}$. 分析 分三种情形讨论求解即可.
解答 解:①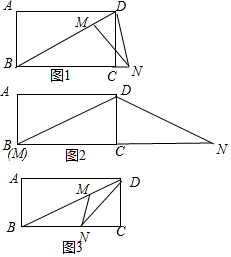 如图1中,当NM=ND时,
如图1中,当NM=ND时,
∴∠NDM=∠NMD,
∵∠MND=∠CBD,
∴∠BDN=∠BND,
∴BD=BN=$\sqrt{B{C}^{2}+C{D}^{2}}$=25.
②如图2中,当DM=DN时,易知M与B重合,此时BC=CN=20,BN=40,
③如图3中,当MN=MD时,易证BN=DN,设BN=DN=x,
在Rt△DNC中,∵DN2=CN2+CD2,
∴x2=(20-x)2+152,
∴x=$\frac{125}{8}$,
故答案为25,40,$\frac{125}{8}$.
点评 本题考查矩形的性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,注意不能漏解.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com