
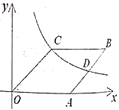
【题目】如图,在平行四边形![]() 中,
中,![]() =45°,点
=45°,点![]() 在
在![]() 轴上,点
轴上,点![]() 是
是![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过
的图象经过![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
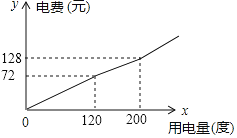
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() (
(![]() ),解答下列问题:
),解答下列问题:
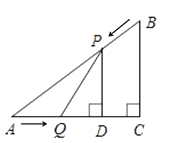
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值;
的最大值;
(2)当![]() 的值为________________时,
的值为________________时,![]() 是等腰三角形
是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
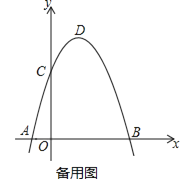
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c为常数a≠0)与x轴,y轴分别交于A,B,C三点,已知A(-1,0),B(3,0),C(0,3),动点E从抛物线的顶点点D出发沿线段DB向终点B运动.
(1)直接写出抛物线解析式和顶点D的坐标;
(2)过点E作EF⊥y轴于点F,交抛物线对称轴左侧的部分于点G,交直线BC于点H,过点H作HP⊥x轴于点P,连接PF,求当线段PF最短时G点的坐标;
(3)在点E运动的同时,另一个动点Q从点B出发沿直线x=3向上运动,点E的速度为每秒![]() 个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.
个单位长度,点Q速度均为每秒1个单位长度,当点E到达终点B时点Q也随之停止运动,设点E的运动时间为t秒,试问存在几个t值能使△BEQ为等腰三角形?并直接写出相应t值.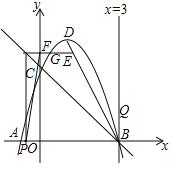
查看答案和解析>>
科目:初中数学 来源: 题型:
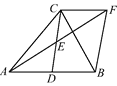
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,与
的左侧,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点.
下方抛物线上的一个动点.
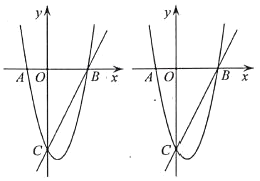
(1)求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() ,并将
,并将![]() 沿
沿![]() 轴对折,得到四边形
轴对折,得到四边形![]() .是否存在点
.是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时点
为菱形?若存在,求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时点
的面积最大?求出此时点![]() 的坐标和四边形
的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查我市民上班时最常用的交通工具的情况随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车;E.其他”中选择最常用的一项.将所有调查结果整理后绘制成如下不完整计图,请结合统计图回答下列问题:
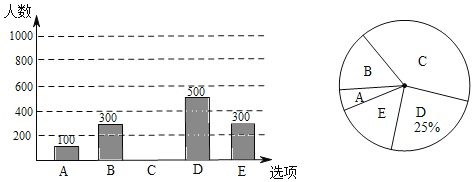
(1)本次一共调查了 名市民;扇形统计图中B项对应的圆心角是 度;
(2)补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com