
 问题再现:
问题再现:分析 (1)尝试解决:如图:边长为a,b的两个正方形,边保持平行,从大正方形中剪去小正方形,剩下的图形可以分割成2个长方形并拼成一个大长方形.根据第一个图形的阴影部分的面积是a2-b2,第二个图形的阴影部分的面积是(a+b)(a-b),可以验证平方差公式;
(2)尝试解决:如图,A表示一个1×1的正方形,B、C、D表示2个2×2的正方形,E、F、G表示3个3×3的正方形,而A、B、C、D、E、F、G恰好可以拼成一个边长为(1+2+3)的大正方形,根据大正方形面积的两种表示方法,可以得出13+23+33=62;
(3)问题拓广:由上面表示几何图形的面积探究知,13+23+33+…+n3=(1+2+3+…+n)2,进一步化简即可.
解答 解:(1)∵如图,左图的阴影部分的面积是a2-b2,
右图的阴影部分的面积是(a+b)(a-b),
∴a2-b2=(a+b)(a-b),
这就验证了平方差公式;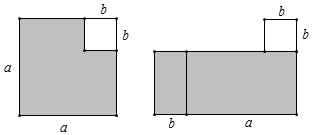
(2)如图,A表示1个1×1的正方形,即1×1×1=13;
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,
因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23;
G与H,E与F和I可以表示3个3×3的正方形,即3×3×3=33;
而整个图形恰好可以拼成一个(1+2+3)×(1+2+3)的大正方形,
由此可得:13+23+33=(1+2+3)2=62;
故答案为:62;
(3)由上面表示几何图形的面积探究可知,13+23+33+…+n3=(1+2+3+…+n)2,
又∵1+2+3+…+n=$\frac{1}{2}$n(n+1),
∴13+23+33+…+n3=[$\frac{1}{2}$n(n+1)]2.
故答案为:[$\frac{1}{2}$n(n+1)]2.
点评 此题主要考查了平方差公式的几何背景,熟练掌握通过不同的方法计算同一个图形的面积来证明一些公式的方法,利用数形结合是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:判断题
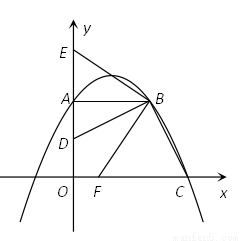
如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连结EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
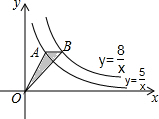 如图,点A、点B分别在反比例函数y=$\frac{5}{x}$和y=$\frac{8}{x}$的图象上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.
如图,点A、点B分别在反比例函数y=$\frac{5}{x}$和y=$\frac{8}{x}$的图象上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
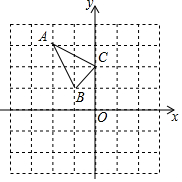 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com