
 如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=
如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=| k | x |
| k |
| x |
| k |
| 2 |
| k |
| 2 |
| k |
| 4 |
| k |
| x |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 4 |
| k |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| k |
| 2 |
| k |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |
| k |
| 4 |
| k |
| 2 |
| 1 |
| 16 |
| k |
| 2 |
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 16 |
| k |
| 2 |
| k |
| 4 |


科目:初中数学 来源: 题型:
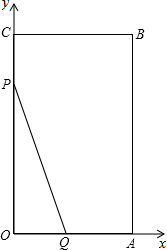 已知:在平面直角坐标系中矩形OABC如图,且A(6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动t秒,且速度均为每秒2个单位长度,设S△OPQ=S.
已知:在平面直角坐标系中矩形OABC如图,且A(6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动t秒,且速度均为每秒2个单位长度,设S△OPQ=S.查看答案和解析>>
科目:初中数学 来源: 题型:
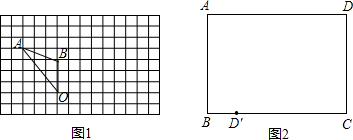
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(带解析) 题型:解答题
①如图1,在每个小方格都是边长为1个单位长度的正方形方格纸中有△OAB,
请将△OAB绕点O顺时针旋转90°,画出旋转后的△OA’B’;
②折纸:有一张矩形纸片ABCD(如图2),要将点D沿某条直线翻折180°,恰好落在BC边上的点D’
处,,请在图中作出该直线。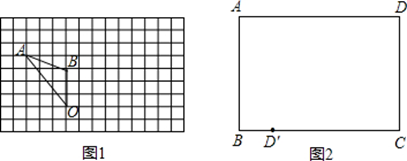
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
①如图1,在每个小方格都是边长为1个单位长度的正方形方格纸中有△OAB,
请将△OAB绕点O顺时针旋转90°,画出旋转后的△OA’B’;
②折纸:有一张矩形纸片ABCD(如图2),要将点D沿某条直线翻折180°,恰好落在BC边上的点D’
处,,请在图中作出该直线。
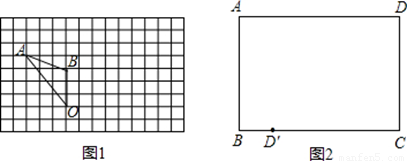
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省九年级上学期期中考试数学卷(A) 题型:解答题
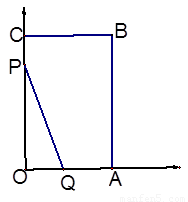
已知:在平面直角坐标系中矩形OABC如图,且A (6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动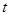 秒,且速度均为每秒2个单位长度,设
秒,且速度均为每秒2个单位长度,设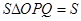 .
.
1.已知直线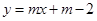 平分矩形OABC面积,求
平分矩形OABC面积,求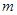 的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
2.当P点在CO上、Q点在OA上时,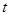 为何值有S=12.?
为何值有S=12.?
3.求在此运动过程中S与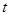 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com