
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是

A.①②③ B.①②④ C.②③④ D.①②③④
【答案】B
【解析】
试题∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF。
由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC。
∵BF平分∠EBC,∴CF=MF。∴DF=CF。故①正确。
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC。
∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN。
∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN。故②正确。
∵在△DEF和△CNF中,易由ASA得△DEF≌△CNF,∴EF=FN。∴BE=BN。
但无法求得△BEN各角的度数,
∴△BEN不一定是等边三角形。故③错误。
∵∠BEM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM。∴BM=3EM。
∴S△BEF=3S△EMF=3S△DEF。故④正确。
综上所述,正确的结论是①②④。故选B。


科目:初中数学 来源: 题型:
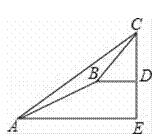
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
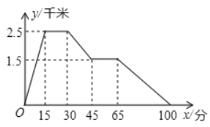
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字![]() ,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字
,另一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字![]() (如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一个人口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
⑴.用树状图或列表法求出小颖参加比赛的概率;
⑵.你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏的规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
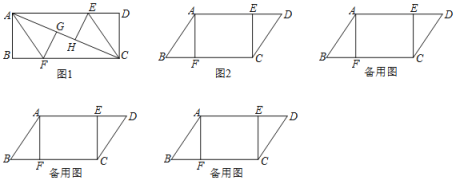
【题目】(1)如图1,长方形ABCD中分别沿AF、CE将AC两侧折叠,使点B、D分别落在AC上的G、H处,则线段AE______CF.(填“>”“<”或“=”)
(2)如图2,在平行四边形ABCD中,△ABF≌△CDE,AB=10cm,BF=6cm,AF=8cm,动点P、Q分别从A、C两点同时出发,点P自A→F→B→A停止,点Q自C→D→E→C停止.
①若点P的速度为每秒5cm,点Q的速度为每秒4cm,设运动时间为t秒.当点P在FB上运动,而点Q在DE上运动时,若四边形APCQ是平行四边形,求此时t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),利用备用图探究,当a与b满足什么数量关系时,四边形APCQ是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
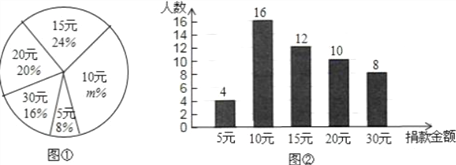
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3副乒乓球拍和2副羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元?
(2)若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如:![]() ,
,![]() ,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:![]() ,
, .
.
像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决下列问题:
(1)将![]() 分母有理化得 ;
分母有理化得 ;![]() 的有理化因式是 ;
的有理化因式是 ;
(2)化简:![]() = ;
= ;
(3)化简:![]() ……+
……+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买20张课桌和一批椅子,该校了解到甲、乙两家商场以同样的价格出售同一型号的课桌与椅子,课桌报价200元/张,椅子报价50元/把.甲、乙两商场分别给出了不同的优惠方案.甲商场的优惠方案:凡买一张课桌赠送一把椅子;乙商场的优惠方案:所有课桌和椅子均按报价的九折销售.若该校需要![]() 把椅子,在甲商场购买所花费用为
把椅子,在甲商场购买所花费用为![]() (元),在乙商场购买所花总费用为
(元),在乙商场购买所花总费用为![]() (元).
(元).
(1)请分别写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该校计划用8100元购买课桌和椅子,选甲、乙哪一家商场可以购买到尽可能多的椅子,说明理由;
(3)该校选择甲、乙哪一家商场花费较少?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com