
 x+b经过点B(-
x+b经过点B(- ,2),且与x轴交于点A,将抛物线y=
,2),且与x轴交于点A,将抛物线y= x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P. x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
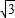 ,2)在直线y=
,2)在直线y=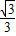 x+b上,所以把B点坐标代入解析式即可求出未知数的值,进而求出其解析式.根据直线解析式可求出A点的坐标及直线与y轴交点的坐标,根据锐角三角函数的定义即可求出∠BAO的度数.
x+b上,所以把B点坐标代入解析式即可求出未知数的值,进而求出其解析式.根据直线解析式可求出A点的坐标及直线与y轴交点的坐标,根据锐角三角函数的定义即可求出∠BAO的度数.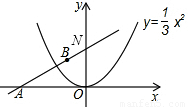 解:(1)设直线与y轴交于点N,
解:(1)设直线与y轴交于点N, ,y=2代入y=
,y=2代入y=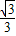 x+b得b=3,
x+b得b=3,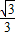 x+3,
x+3,
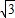 ,0),N(0,3);
,0),N(0,3);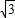 ,ON=3,
,ON=3, =
=
 (x-t)2,则P(t,0),E(0,
(x-t)2,则P(t,0),E(0, t2),
t2), t2),
t2), t2代入y=
t2代入y=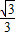 x+3
x+3 t+3=
t+3= t2
t2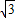 ,t2=3
,t2=3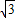 (1分)
(1分) (x+
(x+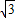 )2或y=
)2或y= (x-3
(x-3 )2;
)2; (x-m)2,AP=3
(x-m)2,AP=3 +m,
+m, (3
(3 +m),
+m),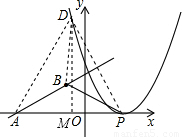
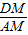 =
= ,
, (9+
(9+ m),
m), (3
(3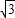 +m)-t=
+m)-t= (3
(3 -m),
-m), (3
(3 -m),0],
-m),0], (3
(3 -m),
-m), (9+
(9+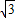 m)],
m)], (9+
(9+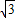 m)=
m)= [-
[- (3
(3 -m)-m2,即m2=27,m=±3
-m)-m2,即m2=27,m=±3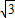 ;
; 时,此时点P(-3
时,此时点P(-3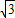 ,0),点P与点A重合,不能构成三角形,不符合题意,舍去.
,0),点P与点A重合,不能构成三角形,不符合题意,舍去. 时P为(3
时P为(3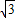 ,0)此时可以构成△DAB,
,0)此时可以构成△DAB, ,0),
,0), ,0).
,0).

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 x+b经过点B(-
x+b经过点B(- ,2),且与x轴交于点A,将抛物线y=
,2),且与x轴交于点A,将抛物线y= x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P. x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.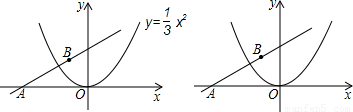
查看答案和解析>>
科目:初中数学 来源:2009年湖北省黄石市中考数学调研试卷(解析版) 题型:解答题
 x+b经过点B(-
x+b经过点B(- ,2),且与x轴交于点A,将抛物线y=
,2),且与x轴交于点A,将抛物线y= x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P. x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
x2平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《图形的相似》(07)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年江苏省江阴市中考数学模拟试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com