
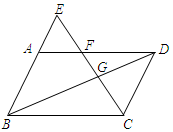
 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设$\overrightarrow{BA}$=$\overrightarrow a$,$\overrightarrow{BC}$=$\overrightarrow b$.
如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设$\overrightarrow{BA}$=$\overrightarrow a$,$\overrightarrow{BC}$=$\overrightarrow b$.分析 (1)根据AE=$\frac{1}{3}$BA即可求出$\overrightarrow{AE}$,根据$\overrightarrow{EC}$=$\overrightarrow{EB}$+$\overrightarrow{BC}$即可求出$\overrightarrow{EC}$,先证明EG=$\frac{4}{7}$EC,即可求出$\overrightarrow{EG}$
(2)首先过点G作GM∥AB,NN∥BC,根据平行四边形法则即可求得答案.
解答 解:(1)∵$\overrightarrow{BA}$=$\overrightarrow{a}$,AE=$\frac{1}{3}$BA,
∴$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{a}$,
∵$\overrightarrow{EC}$=$\overrightarrow{EB}$+$\overrightarrow{BC}$,EB=-$\frac{4}{3}$$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{EC}$=$\overrightarrow{b}$-$\frac{4}{3}$$\overrightarrow{a}$,
∵CD∥EB,
∴EG:CG=EB:CD=4:3,
∴EG:EC=4:7,
∴$\overrightarrow{EG}$=$\frac{4}{7}$$\overrightarrow{b}$-$\frac{16}{21}$$\overrightarrow{a}$,
故答案分别为$\frac{1}{3}$$\overrightarrow{a}$,$\overrightarrow{b}$-$\frac{4}{3}$$\overrightarrow{a}$,$\frac{4}{7}$$\overrightarrow{b}$-$\frac{16}{21}$$\overrightarrow{a}$.
(2)点G作GM∥AB交BC于M,NN∥BC交AB于N,则向量$\overrightarrow{BN}$、$\overrightarrow{BM}$是向量$\overrightarrow{BG}$分别在$\overrightarrow a$、$\overrightarrow b$方向上的分向量.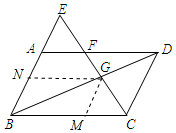
点评 此题考查了平面向量的知识以及平行四边形的性质.注意掌握平行四边形法则与三角形法则的应用是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4米 | B. | 5米 | C. | 6米 | D. | 7米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
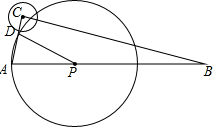 如图,在Rt△ABC中,∠ACB=90°,AC=4,cosA=$\frac{1}{4}$,点P是AB上的动点,以PA为半径作⊙P.若⊙C的半径等于1,且⊙P与⊙C的公共弦长为$\sqrt{2}$,求AP的长.
如图,在Rt△ABC中,∠ACB=90°,AC=4,cosA=$\frac{1}{4}$,点P是AB上的动点,以PA为半径作⊙P.若⊙C的半径等于1,且⊙P与⊙C的公共弦长为$\sqrt{2}$,求AP的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com