
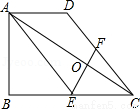
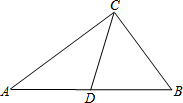
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
(1)求证:AO•OF=OC•OE;
(2)若点F是DC的中点,联结BD交AE于点G,求证:四边形EFDG是菱形.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由BC=2AD,点E是BC的中点,可得AD=CE,又由AD∥BC,可得四边形AECD是平行四边形,即可得AE∥CD,继而证得△AOE∽△COF,即可判定AO•OF=OC•OE;
(2)易得EF是△BCD的中位线,则可判定四边形EFDG是平行四边形,又由直角三角形斜边上的中线的性质,证得DG=EG,继而证得四边形EFDG是菱形.
试题解析:(1)∵BC=2AD,点E是BC的中点,
∴AD=EC=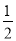 BC,
BC,
∵在梯形ABCD中,AD∥BC,
∴四边形AECD是平行四边形,
∴AE∥CD,
∴△AOE∽△COF,
∴OA:OC=OE:OF,
∴AO•OF=OC•OE;
(2)∵E是BC的中点,F是CD的中点,
∴EF是△BCD的中位线,
∴EF∥BD,
∵AE∥CD,
∴四边形EFDG是平行四边形,
∵AD∥BC,
∴△ADG∽△EBG,
∴DG:BG=AD:EB=AG:EG,
∵AD=BE=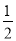 BC,
BC,
∴AG=EG,DG=BG,
∵∠ABC=90°,
∴BG=GE=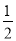 AE,
AE,
∴EG=DG,
∴四边形EFDG是菱形.

考点:1.相似三角形的判定与性质;2.菱形的判定;3.梯形.


科目:初中数学 来源:2013-2014学年上海市松江区中考二模数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线A′处,点D落在点D′处,则D′B长为
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:选择题
下列关于x的方程一定有实数解的是( )
A.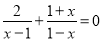 B.
B.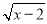 =1-x
=1-x
C.x2-x-1=0 D.x2-x+1=0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:选择题
已知两圆的圆心距是3,它们的半径分别是方程x2-7x+10=0的两个根,那么这两个圆的位置关系是( )
A.内切 B.外切 C.相交 D.外离
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市徐汇区中考二模数学试卷(解析版) 题型:填空题
如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为

查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽省安庆市中考二模数学试卷(解析版) 题型:解答题
为了满足铁路交通的快速发展,安庆火车站从去年开始启动了扩建工程,其中某项工程,甲队单独完成所需时间比乙队单独完成所需时间多5个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍.求甲、乙两队单独完成这项工程各需几个月?
查看答案和解析>>
科目:初中数学 来源:2016届初中数学湘教版七年级上第6章练习卷(解析版) 题型:解答题
为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有 名学生,请估计该校参加“美术”活动项目的人数.
名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com