
已知:函数 (a为常数).
(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A( ,0),B(
,0),B( ,0)两点,与y轴相交于点C,且
,0)两点,与y轴相交于点C,且 .
.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
(1) 或
或 或
或 ;(2)①
;(2)① ;②
;②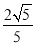 .
.
【解析】
试题分析:(1)根据a取值的不同,有三种情形,需要分类讨论,避免漏解.
(2)①函数与x轴相交于点A( ,0),B(
,0),B( ,0)两点,则
,0)两点,则 ,
, ,满足
,满足 时,方程的根与系数关系.因为
时,方程的根与系数关系.因为 ,则可平方,用
,则可平方,用 ,
, 表示,则得关于a的方程,可求,并得抛物线解析式;
表示,则得关于a的方程,可求,并得抛物线解析式;
②已知解析式则可得A,B,C,D坐标,求sin∠DCB,须作垂线构造直角三角形,结论易得.
试题解析:(1)函数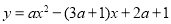 (a为常数),
(a为常数),
若 ,则
,则 ,与坐标轴有两个交点(0,1),(1,0);
,与坐标轴有两个交点(0,1),(1,0);
若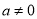 且图象过原点时,
且图象过原点时, ,
, ,有两个交点(0,0),(1,0);
,有两个交点(0,0),(1,0);
若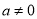 且图象与x轴只有一个交点时,令
且图象与x轴只有一个交点时,令 有:△=
有:△= ,解得
,解得 ,有两个交点(0,﹣1),(1,0),
,有两个交点(0,﹣1),(1,0),
综上得: 或
或 或
或 时,函数图象与坐标轴有两个交点;
时,函数图象与坐标轴有两个交点;
(2)①∵函数与x轴相交于点A( ,0),B(
,0),B( ,0)两点,∴
,0)两点,∴ ,
, 为
为 的两个根,∴
的两个根,∴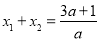 ,
,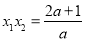 ,∵
,∵ ,∴
,∴ =
= ,解得
,解得 (函数开口向上,
(函数开口向上, ,舍去),或
,舍去),或 ,∴
,∴ ;
;
②∵函数 与x轴相交于点A(
与x轴相交于点A( ,0),B(
,0),B( ,0)两点,与y轴相交于点C,且
,0)两点,与y轴相交于点C,且 ,∴A(1,0),B(3,0),C(0,3),∵D为A关于y轴的对称点,∴D(﹣1,0).根据题意画图,如图1,过点D作DE⊥CB于E,∵OC=3,OB=3,OC⊥OB,∴△OCB为等腰直角三角形,∴∠CBO=45°,∴△EDB为等腰直角三角形,设DE=x,则EB=x,∵DB=4,∴
,∴A(1,0),B(3,0),C(0,3),∵D为A关于y轴的对称点,∴D(﹣1,0).根据题意画图,如图1,过点D作DE⊥CB于E,∵OC=3,OB=3,OC⊥OB,∴△OCB为等腰直角三角形,∴∠CBO=45°,∴△EDB为等腰直角三角形,设DE=x,则EB=x,∵DB=4,∴ ,∴
,∴ ,即DE=
,即DE= .在Rt△COD中,∵DO=1,CO=3,∴CD=
.在Rt△COD中,∵DO=1,CO=3,∴CD= ,∴sin∠DCB=
,∴sin∠DCB=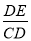 =
=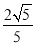 .
.

考点:1.二次函数综合题;2.等腰直角三角形.


科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:填空题
如图,在等边△ABC中,D是边AC上的一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△AED的周长是______.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
若3是关于x的方程 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )
A.-2 B.2 C.-5 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市九年级下学期正月联考数学试卷(解析版) 题型:解答题
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市九年级下学期正月联考数学试卷(解析版) 题型:填空题
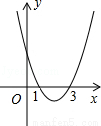
如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 _________ .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:解答题
已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC= AB,则点C表示的数是 ;
AB,则点C表示的数是 ;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=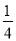 BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com