
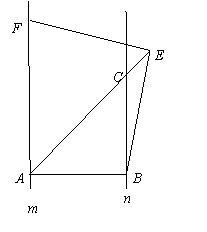
已知点A,B分别是两条平行线m,n上任意两点,C是直线n上一点,且∠ABC=90°,点E在AC的延长线上,BC=kAB (k≠0).
(1)当k=1时,在图(1)中,作∠BEF=∠ABC,EF交直线m于点F.写出线段EF与EB的数量关系,并加以证明;
(2)若k≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,
,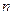 上任意两点,C是直线
上任意两点,C是直线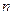 上一点,且
上一点,且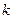 AB (k≠0).
AB (k≠0).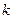 =1时,在图(1)中,作∠BEF=∠ABC,EF交直线
=1时,在图(1)中,作∠BEF=∠ABC,EF交直线 于点F.,写出线段EF与
于点F.,写出线段EF与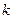 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源:2011届北京市平谷区4月中考数学一模试卷 题型:解答题
已知点A,B分别是两条平行线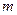 ,
,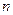 上任意两点,C是直线
上任意两点,C是直线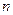 上一点,且
上一点,且
∠ABC=90°,点E在AC的延长线上,BC=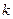 AB (k≠0).
AB (k≠0).
(1)当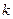 =1
=1 时,在图(1)中,作∠BEF=∠ABC,EF交直线
时,在图(1)中,作∠BEF=∠ABC,EF交直线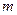 于点F.,写出线段EF与
于点F.,写出线段EF与
EB的数量关系,并加以证明;
(2)若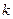 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2013届河北省石家庄市第42中学九年级第一次模拟考试数学试卷(带解析) 题型:解答题
已知点A,B分别是两条平行线m,n上任意两点,C是直线n上一点,且∠ABC=90°,点E在AC的延长线上,BC=kAB(k≠0).
(1)当k=1时,在图(1)中,作∠BEF=∠ABC,EF交直线m于点F.写出线段EF与EB的数量关系,并加以证明;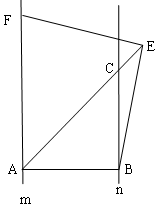
(2)若k≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市考数学一模试卷 题型:解答题
已知点A,B分别是两条平行线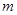 ,
,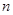 上任意两点,C是直线
上任意两点,C是直线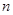 上一点,且
上一点,且
∠ABC=90°,点E在AC的延长线上,BC=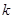 AB (k≠0).
AB (k≠0).
(1)当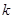 =1时,在图(1)中,作∠BEF=∠ABC,EF交直线
=1时,在图(1)中,作∠BEF=∠ABC,EF交直线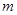 于点F.,写出线段EF与
于点F.,写出线段EF与
EB的数量关系,并加以证明;
(2)若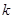 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com