
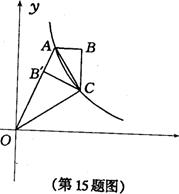
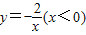 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B'点落在OA上,则四边形OABC的面积是 .
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B'点落在OA上,则四边形OABC的面积是 .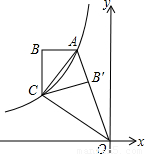
 mn=1,由AB∥x轴,得点A(a-m,2n),由题意得2n(a-m)=-2,从而得出三角形ABC的面积等于
mn=1,由AB∥x轴,得点A(a-m,2n),由题意得2n(a-m)=-2,从而得出三角形ABC的面积等于 an,即可得出答案.
an,即可得出答案. 解:设BC的延长线交x轴于点D,
解:设BC的延长线交x轴于点D,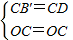 ,
, (x<0)经过四边形OABC的顶点A、C,
(x<0)经过四边形OABC的顶点A、C, |mn|=1,
|mn|=1, an=
an= ,
, +
+ =2.
=2.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
如图,双曲线![]() 经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市亭趾实验学校九年级上期中考试数学试卷(带解析) 题型:填空题
如图,双曲线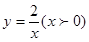 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与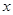 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥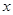 轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.
轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市亭趾实验中学九年级上期中考试数学试卷(解析版) 题型:填空题
如图,双曲线 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与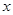 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥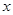 轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.
轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.

查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州江都花荡中学八年级下期末考试数学试卷(解析版) 题型:填空题
如图,双曲线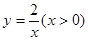 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与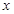 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥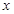 轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是
▲
轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是
▲

查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南驻马店中考二模数学试卷(解析版) 题型:填空题
如图,双曲线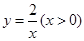 经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com