
【题目】如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水
(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请用尺规作图,将上述两种情况下的自来水厂厂址分别在图(1)(2)中标出,并保留作图痕迹。

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图 ,是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
(1)补全坐标系并指出△ABC和△A'B'C'满足什么几何变换(直接写答案)?
(2)作△A'B'C'关于x轴对称图形△A''B''C'';
(3)△ABC和△A''B''C''满足什么几何变换?求A''、B''、C''三点坐标(直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;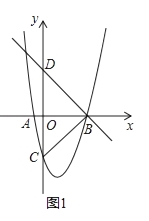
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;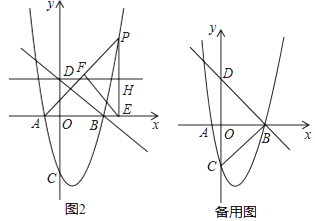
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B与y轴交于C,过C作x轴的平行线交抛物线于点D,过点D作x轴的垂线交x轴于E,点D的坐标为(2,3)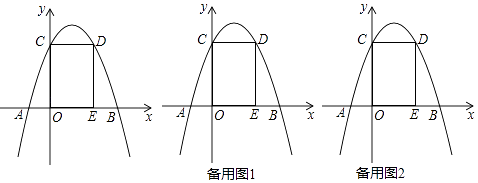
(1)求抛物线的解析式;
(2)点P为第一象限直线DE右侧抛物线上一点,连接AP交y轴于点F,连接PD、DF,设点P的横坐标为t,△PFD的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点P向下平移3个单位得到点Q,连接AQ、EQ,若∠AQE=45°,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.6
B.13
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )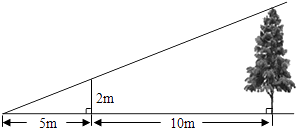
A.5m
B.6m
C.7m
D.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直,展开小桌板后,桌面会保持水平,其中图1、图2分别是小桌板收起时和展开时的实物,图3中的实线是小桌板展开后的示意图,其中OB表示小桌板桌面的宽度,BC表示小桌板的支架,连接OA,此时OA=75厘米,∠AOB=∠ACB=37°,且支架长BC与桌面宽OB的长度之和等于OA的长度,求点B到AC的距离.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)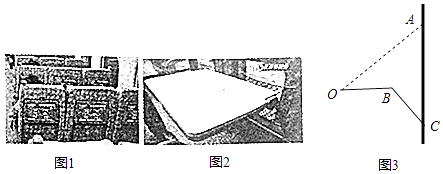
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com