
 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推| 层次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 该层对应的点数 | ||||||
| 所有层的总点数 |
| n(n-1) |
| 2 |
| 层次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 该层对应的点数 | 1 | 6 | 12 | 18 | 24 | 30 |
| 所有层的总点数 | 1 | 7 | 19 | 37 | 61 | 91 |


科目:初中数学 来源: 题型:
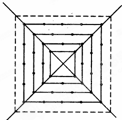 如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.| 层 数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 各层对应的点数 | 4 4 |
8 8 |
12 12 |
16 16 |
20 20 |
4n 4n |
| 所有层的总点数 | 4 4 |
12 12 |
24 24 |
40 40 |
60 60 |
2n(n+1) 2n(n+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推| 层次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 该层对应的点数 | ||||||
| 所有层的总点数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
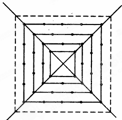 如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
(1)填写下表:
| 层 数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 各层对应的点数 | ______ | ______ | ______ | ______ | ______ | ______ |
| 所有层的总点数 | ______ | ______ | ______ | ______ | ______ | ______ |
(2)写出第n层对应的点数;
(3)写出n层的四边形点阵的总点数;
(4)如果某一层共有79个点,你知道它是第几层吗?
(5)有没有n层的四边形点阵的总点数是180?如果有求出n,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源:湖北省中考真题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com