
分析 (1)根据分式的加减法则把原式进行化简即可;
(2)把b当作已知条件表示出a,再把a的值代入进行计算即可.
解答 解:(1)原式=$\frac{a(a-b)}{{a}^{2}-{b}^{2}}$+$\frac{b(a+b)}{{a}^{2}-{b}^{2}}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$
=$\frac{{a}^{2}-ab+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$
=$\frac{{a}^{2}+{b}^{2}-{a}^{2}}{{a}^{2}-{b}^{2}}$
=$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$;
(2)∵3a=4b,
∴a=$\frac{4b}{3}$,
∴原式=$\frac{{b}^{2}}{\frac{16{b}^{2}}{9}-{b}^{2}}$=$\frac{9}{7}$.
点评 本题考查的是分式的化简求值,在解答此类问题时要注意把分式化为最简形式,再代入求值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
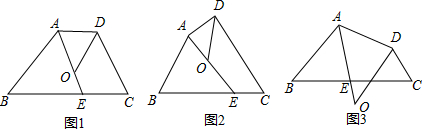
 如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).
如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
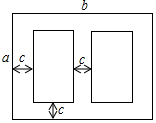 如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com