
分析 (1)先去分母,求出x的值,代入公分母进行检验即可;
(2)先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:(1)方程两边同时乘以x-2得,1-x=-1+x-2,
解得x=2.
检验:将x=2代入原方程,分母x-2=0,
所以,x=2是增根,原方程无解.
(2)原式=$\frac{x-2+1}{x-2}$•$\frac{(x+2)(x-2)}{(x-1)^{2}}$
=$\frac{x-1}{x-2}$•$\frac{(x+2)(x-2)}{{(x-1)}^{2}}$
=$\frac{x+2}{x-1}$,
当x=3时,原式=$\frac{3+2}{3-1}$=$\frac{5}{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
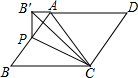 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
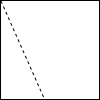 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )| A. | 直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等腰梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
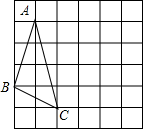 在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分被为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).
在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分被为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com