
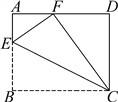
【题目】如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°;
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数.

【答案】(1)见解析;(2)见解析;(3)∠C=50°.
【解析】
(1)求出∠A=∠D,根据平行线的判定推出即可;
(2)求出∠2+∠BHA=180°,根据平行线的判定推出BF∥CE,根据平行线的性质得出即可;
(3)求出∠BEC的度数,根据平行线的性质求出即可.
(1)证明:∵∠A=∠AGE,∠D=∠DGC,
又∵∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD;
(2)证明:∵∠1=∠BHA,∠1+∠2=180°,
∴∠2+∠BHA=180°,
∴BF∥CE,
∴∠BEC+∠B=180°;
(3)∵∠BEC+∠B=180°,∠BEC=2∠B+30°,
∴∠B=50°,∠BEC=130°,
∵AB∥CD,
∴∠C+∠BEC=180°,
∴∠C=50°.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=8cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为
1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:

(1)当t为何值时,PE∥AB?
(2)是否存在某一时刻t,使S△DEQ=![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
(3)如图2连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系,已知![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
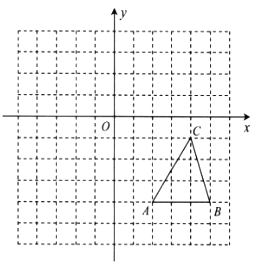
(1)求![]() 的面积;
的面积;
(2)若把![]() 向上平移3个单位长度,再向左平移6个单位长度得到
向上平移3个单位长度,再向左平移6个单位长度得到![]() ,请画出
,请画出![]() ;
;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积与
的面积与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年农历五月初五,是中国民间的传统节日——端午节.它始于我国的春秋战国时期,已列为世界非物质文化遗产.时至今日,端午节在我国仍是一个十分盛行的节日.今年端午节,某地甲、乙两家超市为吸引更多的顾客,开展促销活动,对某种质量和售价相同的粽子分别推出了不同的优惠方案.甲超市的方案是:购买该种粽子超过80元后,超出80元的部分按九折收费;乙超市的方案是:购买该种粽子超过120元后,超出120元的部分按八折收费.请根据顾客购买粽子的金额,选择到哪家超市购买粽子划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足![]() ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD//BC,BD=BC,∠ABC=900;

(1)画出![]() 的高CE;;
的高CE;;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() 平分
平分![]() (
(![]() ),
),![]() 为
为![]() 上一点,且
上一点,且![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,请结合(1)的计算猜想
,请结合(1)的计算猜想![]() 、
、![]() 、
、![]() 之间的数量关系,直接写出答案,不说明理由;(用含有
之间的数量关系,直接写出答案,不说明理由;(用含有![]() 、
、![]() 的式子表示
的式子表示![]() )
)
(3)如图②,当点![]() 在
在![]() 的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com