
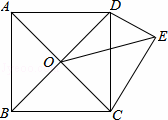
��ͼ��������y=ax2+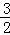 x+c��x�ύ�ڵ�A��4��0����B����1��0������y�ύ�ڵ�C������AC����M���߶�OA�ϵ�һ�����㣨�����O��A�غϣ�������M��MN��AC����OC�ڵ�N������OMN��ֱ��MN�۵�����O�Ķ�Ӧ��O�����ڵ�һ�����ڣ���OM=t����O��MN������AMNC�غϲ������ΪS��
x+c��x�ύ�ڵ�A��4��0����B����1��0������y�ύ�ڵ�C������AC����M���߶�OA�ϵ�һ�����㣨�����O��A�غϣ�������M��MN��AC����OC�ڵ�N������OMN��ֱ��MN�۵�����O�Ķ�Ӧ��O�����ڵ�һ�����ڣ���OM=t����O��MN������AMNC�غϲ������ΪS��
��1���������ߵĽ���ʽ��
��2���ٵ���O������AC��ʱ����ֱ��д����ʱt��ֵ��
����S��t�ĺ�����ϵʽ��
��3���ڵ�M�˶��Ĺ����У���ֱ��д����O��B��C��O��Ϊ������ı��ηֱ��ǵ������κ�ƽ���ı���ʱ����Ӧ��tֵ��
�⣺��1����������y=ax2+ x+c��x�ύ�ڵ�A��4��0����B����1��0����
x+c��x�ύ�ڵ�A��4��0����B����1��0����
�� ��
��
��� ��
��
�������ߵĽ���ʽ��y=�� x2+
x2+ x+2��
x+2��
��2������ͼ1����MN��AC��
���OMN=��O��AM����O��MN=AO��M
�ߡ�OMN=��O��MN��
���AO��M=��O��AM��
��O��M=AM��
��OM=O��M��
��OM=AM=t��
��t= =
=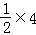 =2��
=2��
���������ߵĽ���ʽ��y=��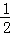 x2+
x2+ x+2��֪C��0��2��
x+2��֪C��0��2��
��A��4��0����C��0��2����
��OA=4��OC=2��
��MN��AC��
��ON��OM=OC��OA=2��4=1��2��
��ON=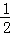 OM=
OM=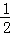 t��
t��
��S=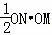 =
= =
=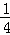 t2��
t2��
��3����ͼ2����B����1��0����C��0��2����
��ֱ��BC��б��Ϊ2��
��OO���BC��
��ֱ��OO��Ľ���ʽΪy=2x��
��O�䣨 m��2m����
m��2m����
��O��N=ON= t��
t��
��O��N2=m2+��2m�� t��2=��
t��2=�� ��2��
��2��
��t=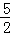 m��
m��
��O��C2=m2+��2��2m��2��
��OB=O��C��
��m2+��2��2m��2=����1��2��
���m1=1��m2= ��
��
��O�䣨1��2���� ��
�� ����
����
��C��0��2����
�൱O�䣨1��2��ʱ����O��B��C��O��Ϊ������ı�����ƽ���ı��Σ���ʱt=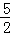 ��
��
��O�䣨 ��
�� ��ʱ����O��B��C��O��Ϊ������ı��������Σ���ʱt=
��ʱ����O��B��C��O��Ϊ������ı��������Σ���ʱt=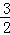 ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ����ֵת������������ͼ���������xΪ81ʱ�����
��y�ǣ� ������
|
| B. 3�� | C��9�� | �ģ�2 |
���� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
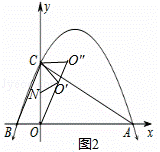
ѧϰίԱͳ��ȫ��50λͬѧ�����ġ���ѧ��Ӣ����������������Ŀ��ϲ����������������ñ���������ͼ�������£�
| ��Ŀ | ���� | ��ѧ | Ӣ�� | ���� | ���� |
| ���� | 10 | a | 15 | 3 | 2 |
��1��������a��ֵΪ��20����
��2����ȫ����ͼ��
��3��С������ϲ������֮һ��С������ϲ������֮һ���ƻ�����ϲ�����������ֵ����У�ÿ��Ŀ��ѡ1�˲μ�ѧУѵ�������б�������ͼ��ʾ���н��������С�С��������1�˱�ѡ�ϵĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������y=��x��3��2+1������ƽ��2����λ��������ƽ��1����λ�õ��������߽���ʽΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�ÿ��С�����εĶ���и�㣬��ABC�͡�DEF�Ķ��㶼�ڸ���ϣ����������ƽ��ֱ������ϵ����������⣺
��1��������ABC����ƽ��4����λ���Ⱥ����õ��ġ�A1B1C1��
��2��������DEF�Ƶ�O��˳ʱ�뷽����ת90������õ��ġ�D1E1F1��
��3����A1B1C1�͡�D1E1F1��ɵ�ͼ������Գ�ͼ��������ǣ���ֱ��д���Գ�������ֱ�ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м�������ȷ���ǣ�������
| �� | A�� |
| B�� |
| C�� | a6=��a3��2 | D�� | b��2=��b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ABCDΪ�����Σ�OΪAC��BD�Ľ��㣬��DCEΪRt������CED=90�㣬��DCE=30�㣬��OE=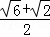 ���������ε����Ϊ��������
��������������������
| �� | A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������37000�ÿ�ѧ��������ʾΪ3.7��10n����n��ֵΪ��������
| �� | A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
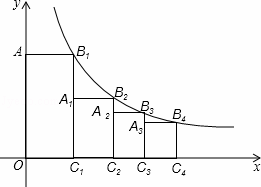
��ͼ����B1�ڷ���������y=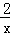 ��x��0����ͼ���ϣ�����B1�ֱ���x���y��Ĵ��ߣ�����ΪC1��A����C1������Ϊ��1��0��ȡx����һ��C2��
��x��0����ͼ���ϣ�����B1�ֱ���x���y��Ĵ��ߣ�����ΪC1��A����C1������Ϊ��1��0��ȡx����һ��C2��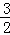 ��0��������C2�ֱ���x��Ĵ��߽�����������ͼ���ڵ�B2����B2���߶�B1C1�Ĵ��߽�B1C1�ڵ�A1��������x����ȡ��C3��2��0����C4��
��0��������C2�ֱ���x��Ĵ��߽�����������ͼ���ڵ�B2����B2���߶�B1C1�Ĵ��߽�B1C1�ڵ�A1��������x����ȡ��C3��2��0����C4��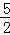 ��0�������˹��������Σ����n�� n��2��nΪ�����������Σ�An��1Cn��1CnBn�����Ϊ������
��0�������˹��������Σ����n�� n��2��nΪ�����������Σ�An��1Cn��1CnBn�����Ϊ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com