
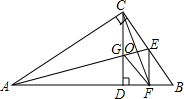
 如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.
如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形. 分析 根据全等三角形的判定定理HL进行证明Rt△AEG≌Rt△AEC(HL),得到GE=EC;根据平行线EG∥CD的性质、∠BAC平分线的性质以及等量代换推知∠FEC=∠CFE,易证CF=CE;从而根据邻边相等的平行四边形是菱形进行判断.
解答 证明:∵∠ACB=90°,
∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,
∴GE=CE.
在Rt△AEG与Rt△AEC中,
$\left\{\begin{array}{l}{GE=CE}\\{AE=AE}\end{array}\right.$,
∴Rt△AEG≌Rt△AEC(HL);
∴GE=EC,
∵CD是AB边上的高,
∴CD⊥AB.
又∵EG⊥AB,
∴EG∥CD,
∴∠CFE=∠GEA.
又由(1)知,Rt△AEG≌Rt△AEC,
∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,
∴CE=CF,
∴GE=EC=FC.
又∵EG∥CD,即GE∥FC,
∴四边形CGFE是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质等知识点.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | $\frac{2}{15}$ | D. | -$\frac{2}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
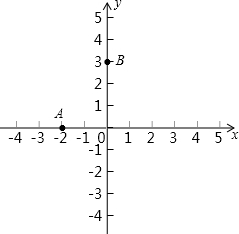 如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.
如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为( )| A. | (1343,0) | B. | (1342,0) | C. | (1343.5,$\frac{\sqrt{3}}{2}$) | D. | (1342.5,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC的三个顶点坐标分别为A(-3,0),B(-2,2),C(-1,2),将△ABC平移至△A1B1C1的位置,点A、B、C对应点分别为A1、B1、C1,点A1的坐标是(1,-2).
△ABC的三个顶点坐标分别为A(-3,0),B(-2,2),C(-1,2),将△ABC平移至△A1B1C1的位置,点A、B、C对应点分别为A1、B1、C1,点A1的坐标是(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
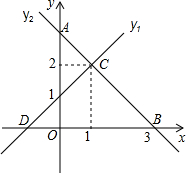 如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)
如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com