
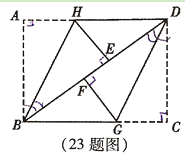
【题目】(10分) 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 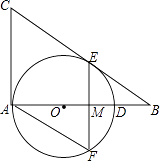
(1)若AC=5,BC=13,求⊙O的半径;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
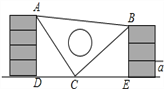
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E. 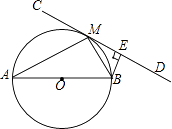
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE= ![]() ,sin∠BAM=
,sin∠BAM= ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )

A. 17 B. 18 C. 19 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.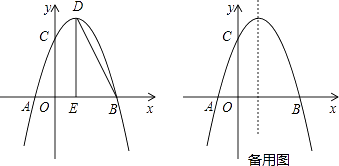
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在平面内,以线段MN为对角线作正方形MPNQ,请直接写出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com