
探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出 的值.
的值. 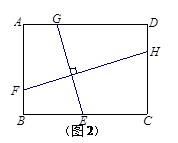
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
(1)证明见解析;
(2)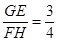 ;
;
(3)不一定成立,图形见解析.
解析试题分析:(1)证明AE=DF,只要证明三角形ABE和DAF全等即可.它们同有一个直角,且AB=AD,又因为∠AEB=90°﹣∠BAE=∠AFD,这样就构成了全等三角形判定中的AAS,两三角形就全等了;
(2)作GM⊥BC于M,FN⊥CD于N,再由GE⊥FH,可得△GME∽△FNH,根据相似性质即可;
(3)不一定成立.
试题解析:(1)∵DF⊥AE,
∴∠AEB=90°﹣∠BAE=∠AFD,
又∵AB=AD,∠ABE=∠DAF=90°,
∴△ABE≌△DAF,
∴AE=DF;
(2)作GM⊥BC于M,FN⊥CD于N,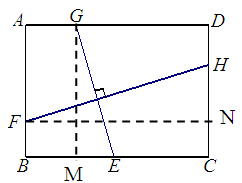
∵GE⊥FH
∴∠MGE=∠NFH,
∴△GME∽△FNH.
∴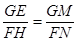 .
.
∵AB=GM=3,FN=BC=4,
∴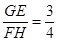 ;
;
(3)不一定成立,如图:
当GE=FH时,GE和FH位置不确定,只有GE=FH=AD时,GE⊥FH.
考点:1.正方形的性质,2.三角形相似.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:解答题
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,小丽在观察某建筑物 .
.
(1)请你根据小亮在阳光下的投影,画出建筑物 在阳光下的投影.
在阳光下的投影.
(2)已知小丽的身高为 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物 的投影长分别为
的投影长分别为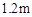 和
和 ,求建筑物
,求建筑物 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题: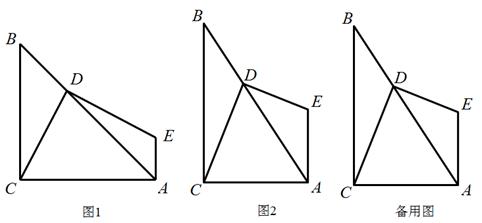
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com