
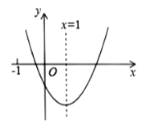
【题目】二次函数![]() (
(![]() )的图象如图所示,对称轴为
)的图象如图所示,对称轴为![]() ,给出下列结论:①
,给出下列结论:①![]() ; ②当
; ②当![]() 时,
时,![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
【答案】①③④
【解析】
根据二次函数图象的开口向上,可得a>0,根据图象与y轴的交点在y轴的负半轴上,可得c<0,根据图象的对称轴是直线x=1,结合a>0可得b<0,进而可得①正确;再根据当x>2时,y有小于0的情况,可判断②错误;因为x=-1时,y>0,∴![]() >0,再结合对称轴可得2a+b=0,进一步可得
>0,再结合对称轴可得2a+b=0,进一步可得![]() ,由此判断③正确;最后由2a+b=0,a>0,可得
,由此判断③正确;最后由2a+b=0,a>0,可得![]() ,所以④正确;到此可得结果.
,所以④正确;到此可得结果.
解:∵二次函数的图象开口向上,∴a>0,
∵二次函数的图象与y轴的交点在y轴的负半轴上,∴c<0,
∵二次函数图象的对称轴是直线x=1,
∴![]() ,∴2a+b=0,b<0.
,∴2a+b=0,b<0.
∴![]() ;故①正确;
;故①正确;
由二次函数的图象可知,抛物线与x轴的右交点的横坐标应大于2小于3,
∴当x>2时,y有小于0的情况,故②错误;
∵当x=-1时,y>0,
∴![]() >0,
>0,
把![]() 代入得:
代入得:![]() ,故③正确;
,故③正确;
前面已得2a+b=0,又∵a>0,∴![]() ,故④正确;
,故④正确;
故答案为:①③④.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)若D为AB的中点,则∠A的度数满足什么条件时,四边形BECD是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
①![]()
②![]()
③![]()
④![]()
(1)请你紧接着写出两个等式:
⑤_____________;
⑥_____________;
(2)根据以上式子的规律,请你写出第![]() 个式子.
个式子.
(3)利用这个规律计算:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
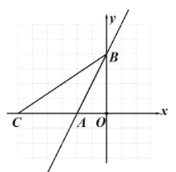
【题目】如图,一次函数y=2x+4的图象分别与x轴,y轴教育点A、点B、点C为x轴一动点。
(1)求A,B两点的坐标;
(2)当ΔABC的面积为6时,求点C的坐标;
(3)平面内是否存在一点D,使四边形ACDB使菱形,若存在,请直接写出点D的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
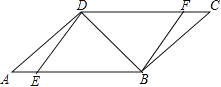
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
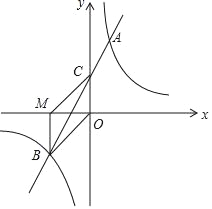
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某垃圾处理厂,对不可回收垃圾的处理费用为90元/吨,可回收垃圾的分拣处理费用也为90元/吨,分拣后再被相关企业回收,回收价格如下表:
垃圾种类 | 纸类 | 塑料类 | 金属类 | 玻璃类 |
回收单价(元/吨) | 500 | 800 | 500 | 200 |
据了解,可回收垃圾占垃圾总量的60%,现有![]() 三个小区12月份产生的垃圾总量分别为100吨,100吨和
三个小区12月份产生的垃圾总量分别为100吨,100吨和![]() 吨.
吨.
(1)已知![]() 小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为
小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为![]() 吨,则
吨,则![]() 小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含
小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含![]() 的代数式表示)
的代数式表示)
(2)![]() 小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
(3)![]() 小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为
小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为![]() 吨,求
吨,求![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
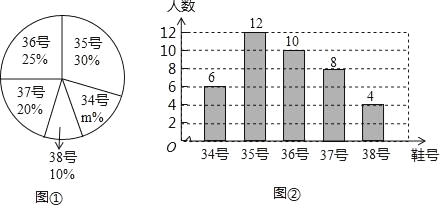
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com