
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是( )

A.②④ B.①④ C.②③ D.①③
【答案】B
【解析】
试题分析:解答本题关键是掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.
由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上得到c>0,由对称轴为x=![]() =-1可以判定②错误;由图象与x轴有交点,对称轴为x=
=-1可以判定②错误;由图象与x轴有交点,对称轴为x=![]() =-1,与y轴的交点在y轴的正半轴上,可以推出b2-4ac>0,即b2>4ac,①正确;由x=-1时y有最大值,由图象可知y≠0,③错误.然后即可作出选择
=-1,与y轴的交点在y轴的正半轴上,可以推出b2-4ac>0,即b2>4ac,①正确;由x=-1时y有最大值,由图象可知y≠0,③错误.然后即可作出选择
①∵图象与x轴有交点,对称轴为x=![]() =-1,与y轴的交点在y轴的正半轴上,
=-1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2-4ac>0,
即b2>4ac,正确;
②∵抛物线的开口向下,
∴a<0,
∵与y轴的交点在y轴的正半轴上,
∴c>0,
∵对称轴为x=![]() =-1,
=-1,
∴2a=b,
∴2a+b=4a,a≠0,
错误;
③∵x=-1时y有最大值,
由图象可知y≠0,错误;
④把x=1,x=-3代入解析式得a+b+c=0,9a-3b+c=0,两边相加整理得
5a-b=-c<0,即5a<b.
故选B.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A. (x﹣1)2=4 B. (x+1)2=4 C. (x﹣1)2=16 D. (x+1)2=16
查看答案和解析>>
科目:初中数学 来源: 题型:
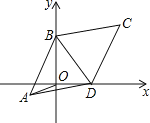
【题目】如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题11分)完成下列推理说明:
(1)如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
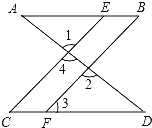
因为∠1=∠2(已知),且∠1=∠4(___________)
所以∠2=∠4(等量代换)
所以CE∥BF(___________)
所以∠___=∠3(_________________)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(______________________))
(2)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
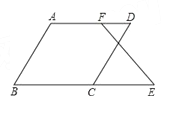
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (__________)
∴∠B= ____(_______________________)
又∵∠B=∠D( 已知 ),
∴ ∠_____= ∠__________ ( 等量代换 )
∴AD∥BE(_____________________)
∴∠E=∠DFE(_____________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com