
| A. | -a>-b | B. | -a+1>b+1 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac<bc |
分析 根据不等式的性质,逐一判断可得答案.
解答 解:A、根据不等式的基本性质3,两边都乘以-1得:-a>-b,故此选项正确;
B、当a=1、b=2时,-a+1<b+1,故此选项错误;
C、当a=-1、b=1时,$\frac{1}{a}$<$\frac{1}{b}$,故此选项错误;
D、当c<0时,由不等式性质3可得ac>bc,故此选项错误;
故选:A.
点评 本题考查了不等式的性质,主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
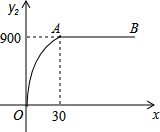 成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).
成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x≥1 | C. | x≥1且x≠3 | D. | x≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30,27 | B. | 30,29 | C. | 29,30 | D. | 30,28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com